
分析 (1)通过4Sn=an2+2an,令n=1可得首项,当n≥2时,利用4an=an2+2an-(an-12+2an-1)可得公差,进而可得结论;
(Ⅱ)通过令n=1可得T1<$\frac{9}{32}$满足结论,当n≥2时,利用放缩法可得$\frac{n+3}{{{a}_{n}}^{3}•{2}^{n}}$<$\frac{1}{8}$[$\frac{1}{(n-1)n}$•$\frac{1}{{2}^{n-1}}$-$\frac{1}{n(n+1)}$•$\frac{1}{{2}^{n}}$],并项相加即得.
解答 (1)解:当n=1时,4a1=4S1=${{a}_{1}}^{2}$+2a1,
解得a1=2或a1=0(舍去);
当n≥2时,4Sn=an2+2an,4Sn-1=an-12+2an-1,
相减得4an=an2+2an-(an-12+2an-1),即an2-an-12=2(an+an-1),
又an>0,∴an+an-1≠0,则an-an-1=2,
∴数列{an}是首项为2,公差为2的等差数列,
∴an=2n;
(Ⅱ)证明:当n=1时,T1=$\frac{n+3}{{{a}_{n}}^{3}•{2}^{n}}$=$\frac{1}{4}$=$\frac{8}{32}$<$\frac{9}{32}$;
当n≥2时,$\frac{n+3}{{{a}_{n}}^{3}•{2}^{n}}$=$\frac{n+3}{8{n}^{3}•{2}^{n}}$=$\frac{n+3}{8n•{n}^{2}•{2}^{n}}$
<$\frac{n+3}{8n({n}^{2}-1)•{2}^{n}}$=$\frac{n+3}{8(n-1)n(n+1)•{2}^{n}}$=$\frac{1}{8}$•$\frac{n+1+2}{(n-1)n(n+1)•{2}^{n}}$
=$\frac{1}{8}${$\frac{1}{(n-1)n•{2}^{n}}$+[$\frac{1}{(n-1)n}$-$\frac{1}{n(n+1)}$]$\frac{1}{{2}^{n}}$}
=$\frac{1}{8}$[$\frac{1}{(n-1)n}$•$\frac{1}{{2}^{n-1}}$-$\frac{1}{n(n+1)}$•$\frac{1}{{2}^{n}}$],
∴Tn<$\frac{1}{4}$+$\frac{1}{8}$[$\frac{1}{1×2×{2}^{1}}$-$\frac{1}{2×3×{2}^{2}}$+$\frac{1}{2×3×{2}^{2}}$-$\frac{1}{3×4×{2}^{3}}$+…+$\frac{1}{(n-1)n}$•$\frac{1}{{2}^{n-1}}$-$\frac{1}{n(n+1)}$•$\frac{1}{{2}^{n}}$]
=$\frac{1}{4}$+$\frac{1}{8}$($\frac{1}{1×2×{2}^{1}}$-$\frac{1}{n(n+1)}$•$\frac{1}{{2}^{n}}$)
<$\frac{1}{4}$+$\frac{1}{8}$•$\frac{1}{1×2×{2}^{1}}$
=$\frac{1}{4}$+$\frac{1}{32}$=$\frac{9}{32}$;
综上,对任意n∈N*,均有Tn<$\frac{9}{32}$成立.
点评 本题考查求数列的通项、判断数列和的取值范围,注意解题方法的积累,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | {0,1,2} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图一个倒三角形数表:
如图一个倒三角形数表:| A. | $\sqrt{2}$-1 | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
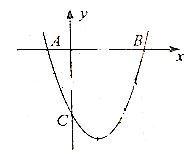 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com