
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
分析 先画出分段函数的图象,根据图象确定字母a、b、c的取值范围,最后数形结合写出其取值范围即可
解答 解:由g(x)=f(x)-m=0得m=f(x),
若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,
即等价为函数y=f(x)与y=m有三个互不相同的交点,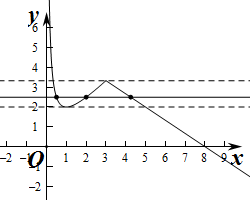
作出函数f(x)的图象如图:
当x>3时,f(x)=$-\frac{2}{3}x+\frac{16}{3}$≤$-\frac{2}{3}×3+\frac{16}{3}$=$\frac{10}{3}$,
∵函数f(x)=x+$\frac{1}{x}$在(0,1]上递减,在[1,3]上递增,
∴2≤f(x)≤$\frac{10}{3}$,
∴若函数y=f(x)与y=m有三个互不相同的交点,
则2<m<$\frac{10}{3}$,
设a<b<c,
由f(x)=x+$\frac{1}{x}$=$\frac{10}{3}$,
解得x=$\frac{1}{3}$或x=3,
由f(x)=$-\frac{2}{3}x+\frac{16}{3}$=2,解得x=5,
则$\frac{1}{3}$<a<1,1<b<3,3<c<5,
当0<x≤3时,由g(x)=f(x)-m=x+$\frac{1}{x}$-m=$\frac{{x}^{2}-mx+1}{x}$=0得x2-mx+1=0,
则ab=1,
故abc=c,
即abc的范围就是c的范围是(3,5),
故选:D
点评 本题考查了分段函数图象的画法及其应用,对数函数及一次函数图象的画法,数形结合求参数的取值范围,画出分段函数图象并数形结合解决问题是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{π}{4})$ | B. | $(-π,-\frac{π}{2})$ | C. | $(\frac{3π}{4},2π)$ | D. | $(-\frac{π}{2},-\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{4}})∪({\frac{{\sqrt{2}}}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[{\frac{1}{2},2\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com