
| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2 |
分析 设$\overrightarrow{PA}=\overrightarrow{a},\overrightarrow{PB}=\overrightarrow{b},\overrightarrow{PC}=\overrightarrow{c}$,根据条件以及数量积公式,即可得到$|\overrightarrow{a}||\overrightarrow{b}|$+$|\overrightarrow{b}||\overrightarrow{c}|$+$|\overrightarrow{c}||\overrightarrow{a}|$=18,连接CM,延长之后交AB的中点D,连接PD,根据向量加法的几何意义及重心的性质便可得到$\overrightarrow{PM}=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$,只要求出$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$的最小值即可.
解答 解:设$\overrightarrow{PA}=\overrightarrow{a},\overrightarrow{PB}=\overrightarrow{b},\overrightarrow{PC}=\overrightarrow{c}$,根据条件以及数量积公式,即可得到$|\overrightarrow{a}||\overrightarrow{b}|$+$|\overrightarrow{b}||\overrightarrow{c}|$+$|\overrightarrow{c}||\overrightarrow{a}|$=18,连接CM,延长之后交AB的中点D,连接PD,D为AB中点,所以$\overrightarrow{PM}=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$,
所以|$\overrightarrow{PM}|=\frac{1}{3}|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$,
∴$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}{|}^{2}={\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}+2\overrightarrow{a}•\overrightarrow{c}+2\overrightarrow{b}•\overrightarrow{c}$=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}+18$,
因为${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}≥2|\overrightarrow{a}||\overrightarrow{b}|$,${\overrightarrow{a}}^{2}+{\overrightarrow{c}}^{2}≥2|\overrightarrow{a}||\overrightarrow{c}|$,${\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}≥2|\overrightarrow{b}||\overrightarrow{c}|$,
相加得到${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}≥|\overrightarrow{a}||\overrightarrow{b}|+|\overrightarrow{a}||\overrightarrow{c}|+|\overrightarrow{b}||\overrightarrow{c}|$=18,
所以${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}≥18$,
所以$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}{|}^{2}≥36$,
所以$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|≥6$;
∴$|\overrightarrow{PM}|≥$2;
故选D.
点评 本题考查向量数量积的计算公式,向量加法、数乘的几何意义,向量加法的平行四边形法则,重心的性质:重心到顶点距离是它到对边中点距离的2倍,以及基本不等式的应用


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
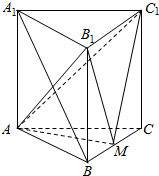 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移π个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | log310+3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图一个倒三角形数表:
如图一个倒三角形数表:| A. | $\sqrt{2}$-1 | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com