
 如图一个倒三角形数表:
如图一个倒三角形数表:| A. | $\sqrt{2}$-1 | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由已知中a1.j=xj-1(j=1,2,…,101),ai.j=$\frac{{a}_{i-1,j}+{a}_{i-1,j+1}}{2}$,可得ai.1=($\frac{x+1}{2}$)i-1,再由x>0,a101.1=$\frac{1}{{2}^{50}}$,可得答案.
解答 解:∵a1.j=xj-1(j=1,2,…,101),
∴a1.1=1,a1.2=x,a1.3=x2,a1.4=x3,…,a1.101=x100,
a2.1=$\frac{x+1}{2}$,a2.2=$\frac{x+1}{2}$•x,a2.3=$\frac{x+1}{2}$•x2,a2.4=$\frac{x+1}{2}$•x3,…,a2.100=$\frac{x+1}{2}$•x99,
a3.1=($\frac{x+1}{2}$)2,a3.2=($\frac{x+1}{2}$)2•x,a3.3=($\frac{x+1}{2}$)2•x2,a3.4=($\frac{x+1}{2}$)2•x3,…,a3.99=($\frac{x+1}{2}$)2•x98,
a4.1=($\frac{x+1}{2}$)3,a4.2=($\frac{x+1}{2}$)3•x,a4.3=($\frac{x+1}{2}$)3•x2,a4.4=($\frac{x+1}{2}$)3•x3,…,a4.98=($\frac{x+1}{2}$)3•x97,
…
a99.1=($\frac{x+1}{2}$)98,a99.2=($\frac{x+1}{2}$)98•x,a99.3=($\frac{x+1}{2}$)98•x2,
a100.1=($\frac{x+1}{2}$)99,a100.2=($\frac{x+1}{2}$)99•x,
a101.1=($\frac{x+1}{2}$)100,
又由a101.1=$\frac{1}{{2}^{50}}$,
∴($\frac{x+1}{2}$)100=$\frac{1}{{2}^{50}}$,
解得:x+1=±$\sqrt{2}$,
即x=$\sqrt{2}$-1,或x=-$\sqrt{2}$-1(舍去),
故选:A
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
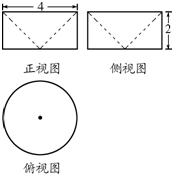
| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com