
分析 根据条件分别求出函数在x>0时,对应的解析式,根据函数奇偶性的性质转化为当x>0时,若直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,利用数形结合进行求解即可.
解答 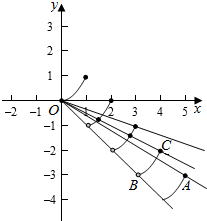 解:∵当0<x≤1时,f(x)=x2,
解:∵当0<x≤1时,f(x)=x2,
∴f(1)=1,
则当x>0时,f(x+1)=f(x)+f(1)=f(x)+1,
即f(x)=f(x-1)-1,
若1<x≤2,则0<x-1≤1,
则f(x)=f(x-1)-1=(x-1)2-1=x2-2x,1<x≤2,
若2<x≤3,则1<x-1≤2,
则f(x)=f(x-1)-1=(x-1)2-2(x-1)-1=x2-4x+2,2<x≤3,
若3<x≤4,则2<x-1≤3,
则f(x)=f(x-1)-1=(x-1)2-4(x-1)+2-1=x2-6x+6,3<x≤4,
若4<x≤5,则3<x-1≤4,
则f(x)=f(x-1)-1=(x-1)2-6(x-1)+6-1=x2-8x+12,4<x≤5,
∵f(x)是定义在R上的奇函数,
∴若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,
则等价为当x>0时,若直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
作出函数f(x)在x>0时的图象如图:
则当x=4时,f(4)=42-6×4+6=-2,即C(4,-2),
当x=5时,f(5)=52-8×5+12=-3,即A(5,-3),
当直线y=kx经过点C时,此时当x>0时,两个函数有3个交点,此时k=-$\frac{1}{2}$,
当直线y=kx经过点A时,此时当x>0时,两个函数有4个交点,此时k=-$\frac{3}{5}$,
则若两个函数在x>0时,有3个交点,
则-$\frac{3}{5}$<k≤-$\frac{1}{2}$.
故答案为:-$\frac{3}{5}$<k≤-$\frac{1}{2}$.
点评 本题主要考查函数与方程的应用,根据条件求出函数的解析式,利用数形结合将条件转化为两个函数的交点个数问题是解决本题的关键.综合性较强,比较复杂.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
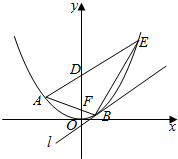 如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com