
分析 (Ⅰ)设“选手甲进入复赛”为事件A,分别求出选手甲答了3题都对进入复赛概率、选手甲答了4个题,前3个2对1错进入复赛的概率和选手甲答了5个题,前4个2对2错进入复赛的概率,由此能求出选手甲进入复赛的概率.
(Ⅱ)X的可能取值为3,4,5,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)设“选手甲进入复赛”为事件A,
则选手甲答了3题都对进入复赛概率为:$C_3^3{(\frac{3}{4})^3}=\frac{27}{64}$;
或选手甲答了4个题,前3个2对1错进入复赛概率为:$C_3^2{(\frac{3}{4})^2}×\frac{1}{4}×\frac{3}{4}=\frac{81}{256}$,
或选手甲答了5个题,前4个2对2错进入复赛概率为:$C_4^2{(\frac{3}{4})^2}•{(\frac{1}{4})^2}×\frac{3}{4}=\frac{81}{512}$,
∴选手甲进入复赛的概率$P(A)=\frac{27}{64}+\frac{81}{256}+\frac{81}{512}=\frac{459}{512}$.…(4分)
(Ⅱ)X的可能取值为3,4,5,对应X的每个取值,选手甲被淘汰或进入复赛的概率,
$P(X=3)=C_3^3{(\frac{3}{4})^3}+C_3^3{(\frac{1}{4})^3}=\frac{7}{16}$…(6分)
$P(X=4)=C_3^2{(\frac{3}{4})^2}×\frac{1}{4}×\frac{3}{4}+C_3^2{(\frac{1}{4})^2}×\frac{3}{4}×\frac{1}{4}=\frac{45}{128}$…(8分)
$P(X=5)=C_4^2{(\frac{3}{4})^2}×{(\frac{1}{4})^2}=\frac{27}{128}$,
X的分布列为:
| X | 3 | 4 | 5 |
| P(X) | $\frac{7}{16}$ | $\frac{45}{128}$ | $\frac{27}{128}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
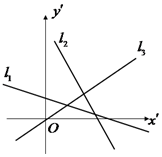 如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下面选项中正确的是( )
如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下面选项中正确的是( )| A. | k3>k1>k2 | B. | k1-k2<0 | C. | k2•k3>0 | D. | k3>k2>k1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [2,+∞) | C. | (0,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数,单调递增区间是(0,+∞) | B. | f(x)是偶函数,单调递减区间是(-∞,1) | ||
| C. | f(x)是奇函数,单调递增区间是(-∞,0) | D. | f(x)是奇函数,单调递减区间是(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km,试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式.
一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km,试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
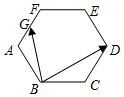
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{7\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{4}}$ | B. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{2}}$ | C. | a${\;}^{\frac{11}{4}}$ | D. | b${\;}^{\frac{11}{4}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com