
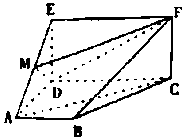
 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.分析 (1)当M是AE线段的中点时,连接CE,交DF于N,连接MN,推导出MN∥AC,由此能证明AC∥平面DMF.
(2)由VM-ADF=VF-MDA,能求出三棱锥M-ADF的体积.
解答 解:(1)当M是AE线段的中点时,AC∥平面DMF,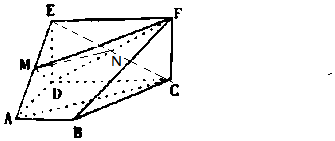 证明如下:
证明如下:
连接CE,交DF于N,连接MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN?平面DMN,又AC?平面DMF,
所以AC∥平面DMF.
(2)∵∠AED=45°,AE=$\sqrt{2}$,
∴AD=DE=1,DC=2,
VM-ADF=VF-MDA,S△MDA=$\frac{1}{2}×1×\frac{1}{2}=\frac{1}{4}$,h=CD=2,
∴三棱锥M-ADF的体积VM-ADF=$\frac{1}{3}×\frac{1}{4}×2$=$\frac{1}{6}$.
点评 本题考查满足线面平行的点的位置的确定与证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{2}}}{2}$,且过点A(2,1).
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{2}}}{2}$,且过点A(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
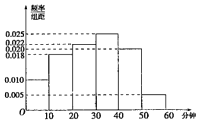 电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:| 非体育迷 | 体育迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
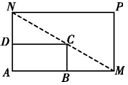 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com