
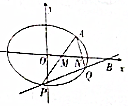
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{2}}}{2}$,且过点A(2,1).
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{2}}}{2}$,且过点A(2,1).分析 (1)根据题意,由椭圆的离心率可得a2=2b2,又由椭圆E过点A(2,1),则$\frac{4}{{2{b^2}}}+\frac{1}{b^2}=1⇒{b^2}=3$,即可得a2、b2的值,将其代入椭圆方程即可得答案;
(2)设直线l的方程为x=my+3,以及P(x1,y1),Q(x2,y2),由P、Q的坐标可得直线AP、AQ的方程,结合题意可得M、N的坐标,联立直线l与椭圆的方程,整理可得(2+m2)y2+6my+3=0,利用根与系数的关系表示|BM|+|BN|的值,化简整理可得答案.
解答 解:(1)根据题意,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,
则有e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{1}{2}$,即a2=2c2⇒a2=2b2,
又由椭圆E过点A(2,1),则$\frac{4}{{2{b^2}}}+\frac{1}{b^2}=1⇒{b^2}=3$,
∴椭圆E的方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$.
(2)设直线l的方程为x=my+3,P(x1,y1),Q(x2,y2),
直线AP的方程为$y-1=\frac{{{y_1}-1}}{{{x_1}-2}}(x-2)$,可得$M(\frac{{2{y_1}-{x_1}}}{{{y_1}-1}},0)$,即$M(\frac{{(2-m){y_1}-3}}{{{y_1}-1}},0)$,
直线AQ的方程为$y-1=\frac{{{y_2}-1}}{{{x_2}-2}}(x-2)$,可得$N(\frac{{2{y_2}-{x_2}}}{{{y_2}-1}},0)$,即$N(\frac{{(2-m){y_2}-3}}{{{y_2}-1}},0)$.
联立$\left\{{\begin{array}{l}{x=my+3}\\{{x^2}+2{y^2}=6}\end{array}}\right.$,消去x,整理得(2+m2)y2+6my+3=0.
由△=36m2-12(2+m2)>0,可得m2>1,
${y_1}+{y_2}=-\frac{6m}{{2+{m^2}}}$,${y_1}{y_2}=\frac{3}{{2+{m^2}}}$,
|BM|+|BN|=$3-\frac{{(2-m){y_1}-3}}{{{y_1}-1}}+3-\frac{{(2-m){y_2}-3}}{{{y_2}-1}}$=$6-\frac{{(2-m){y_1}-3}}{{{y_1}-1}}-\frac{{(2-m){y_2}-3}}{{{y_2}-1}}$,
=6-$\frac{(4-2m){y}_{1}{y}_{2}+(m-5)({y}_{1}+{y}_{2})+6}{{y}_{1}{y}_{2}-({y}_{1}+{y}_{2})+1}$=6-$\frac{24(m+1)}{{m}^{2}+6m+5}$=6-$\frac{24}{m+5}$;
因为m>0,m2>1,所以m>1,
因此$0<\frac{24}{m+5}<4$,即$2<6-\frac{24}{m+5}<6$,
∴|BM|+|BN|的取值范围是(2,6).
点评 本题考查直线与椭圆的位置关系,涉及椭圆的几何性质,关键是先依据题意,求出椭圆的标准方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
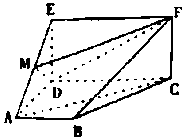 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com