Question

11£®¹ýÍÖÔ²C£º$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$£¨a£¾b£¾0£©ÉÏÒ»µãPÏòxÖá×÷´¹Ïߣ¬´¹×ãΪÓÒ½¹µãF£¬A¡¢B·Ö±ðΪÍÖÔ²CµÄ×󶥵ãºÍÉ϶¥µã£¬ÇÒAB¡ÎOP£¬$|{AF}|=\sqrt{6}+\sqrt{3}$£®
£¨¢ñ£©ÇóÍÖÔ²CµÄ·½³Ì£»
£¨¢ò£©Èô¶¯Ö±ÏßlÓëÍÖÔ²C½»ÓÚM¡¢NÁ½µã£¬ÇÒÒÔMNΪֱ¾¶µÄÔ²ºã¹ý×ø±êÔ­µãO£®ÎÊÊÇ·ñ´æÔÚÒ»¸ö¶¨Ô²Ó붯ֱÏßl×ÜÏàÇУ®Èô´æÔÚ£¬Çó³ö¸Ã¶¨Ô²µÄ·½³Ì£»Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®

Answer 1

·ÖÎö £¨1£©ÓɵãPµÄ×ø±ê¼ÆËã¿ÉµÃK_OPÓëK_AB£¬ÓÖÓÉAB¡ÎOP£¬µÃ$\frac{b^2}{ac}=\frac{b}{a}$£¬»¯¼ò¿ÉµÃb=c£¬$a=\sqrt{2}c$£¬½ø¶øÓÉÍÖÔ²µÄ¼¸ºÎÐÔÖʿɵÃa¡¢bµÄÖµ£¬½«a¡¢bµÄÖµ´úÈë·½³Ì¼´¿ÉµÃ´ð°¸£»
£¨2£©ÏȼÙÉè´æÔÚÕâÑùµÄÔ²£¬·ÖÎö¿ÉµÃx₁x₂+y₁y₂=0£¬°´Ö±ÏßµÄбÂÊ´æÔÚÓë·ñ·ÖÁ½ÖÖÇé¿öÌÖÂÛ£¬Éè³öÖ±Ïߵķ½³Ì£¬Çó³öÔ­µãOµ½Ö±ÏßlµÄ¾àÀ룬ÓÉÖ±ÏßÓëÔ²µÄλÖùØϵ·ÖÎö¿ÉµÃ´ð°¸£®

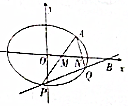
½â´ð ½â£º£¨1£©ÓÉÌâÒâµÃ$P£¨{c£¬\frac{b^2}{a}}£©$£¬ËùÒÔ${k_{OP}}=\frac{b^2}{ac}$£¬${k_{AB}}=\frac{b}{a}$£®
ÓÉAB¡ÎOP£¬µÃ$\frac{b^2}{ac}=\frac{b}{a}$£¬½âµÃb=c£¬$a=\sqrt{2}c$£¬
ÓÉ$|{AF}|=a+c=\sqrt{6}+\sqrt{3}$£¬µÃ$b=c=\sqrt{3}$£¬$a=\sqrt{6}$£¬
ÍÖÔ²CµÄ·½³ÌΪ$\frac{x^2}{6}+\frac{y^2}{3}=1$£®
£¨2£©¼ÙÉè´æÔÚÕâÑùµÄÔ²£®
ÉèM£¨x₁£¬y₁£©£¬N£¨x₂£¬y₂£©£®
ÓÉÒÑÖª£¬ÒÔMNΪֱ¾¶µÄÔ²ºã¹ýÔ­µãO£¬¼´$\overrightarrow{OM}¡Í\overrightarrow{ON}$£¬ËùÒÔx₁x₂+y₁y₂=0£®
µ±Ö±Ïßl´¹Ö±ÓÚxÖáʱ£¬x₁=x₂£¬y₁=-y₂£¬ËùÒÔ$x_1^2-y_1^2=0$£¬
ÓÖ$\frac{x_1^2}{6}+\frac{y_1^2}{3}=1$£¬½âµÃ$x_1^2=y_1^2=2$£¬
²»·ÁÉè$M£¨{\sqrt{2}£¬\sqrt{2}}£©$£¬$N£¨{\sqrt{2}£¬-\sqrt{2}}£©$»ò$M£¨{-\sqrt{2}£¬\sqrt{2}}£©$£¬$N£¨{-\sqrt{2}£¬-\sqrt{2}}£©$£¬
¼´Ö±ÏßlµÄ·½³ÌΪ$x=\sqrt{2}$»ò$x=-\sqrt{2}$£¬
´ËʱԭµãOµ½Ö±ÏßlµÄ¾àÀëΪ$d=\sqrt{2}$£®
µ±Ö±ÏßlµÄбÂÊ´æÔÚʱ£¬¿ÉÉèÖ±ÏßlµÄ·½³ÌΪy=kx+m£¬
½â$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{3}=1\\ y=kx+m\end{array}\right.$ÏûÈ¥yµÃ·½³Ì£º£¨1+2k²£©x²+4kmx+2m²-6=0£¬
ÒòΪֱÏßlÓëÍÖÔ²C½»ÓÚM£¬NÁ½µã£¬
ËùÒÔ·½³ÌµÄÅбðʽ¡÷=£¨4km£©²-4£¨1+2k²£©£¨2m²-6£©£¾0£¬¼´m²£¼3£¨k²+2£©£¬
ÇÒ${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}$£¬${x_1}{x_2}=\frac{{2{m^2}-6}}{{1+2{k^2}}}$£®
ÓÉx₁x₂+y₁y₂=0£¬µÃx₁x₂+£¨kx₁+m£©£¨kx₂+m£©=$£¨{1+{k^2}}£©{x_1}{x_2}+km£¨{{x_1}+{x_2}}£©+{m^2}=0$£¬
ËùÒÔ$£¨{1+{k^2}}£©\frac{{2{m^2}-6}}{{1+2{k^2}}}$$-\frac{{4{k^2}{m^2}}}{{1+2{k^2}}}+{m^2}=0$£¬
ÕûÀíµÃm²=2£¨1+k²£©£¨Âú×ã¡÷£¾0£©£®
ËùÒÔÔ­µãOµ½Ö±ÏßlµÄ¾àÀë$d=\frac{|m|}{{\sqrt{1+{k^2}}}}=\sqrt{2}$£®
×ÛÉÏËùÊö£¬Ô­µãOµ½Ö±ÏßlµÄ¾àÀëΪ¶¨Öµ$\sqrt{2}$£¬¼´´æÔÚ¶¨Ô²x²+y²=2×ÜÓëÖ±ÏßlÏàÇУ®

µãÆÀ ±¾Ì⿼²éÖ±ÏßÓëÍÖÔ²µÄλÖùØϵ£¬Éæ¼°ÍÖÔ²µÄ±ê×¼·½³Ì£¬ÐèÒªÖ±ÏßµÄбÂÊ´æÔÚÓë·ñ½øÐзÖÀàÌÖÂÛ£®