
分析 根据题意可设D(0,0),A(2,0),B(-1,$\sqrt{3}$),C(-1,-$\sqrt{3}$),P(2+cosθ,sinθ),M($\frac{1+cosθ}{2}$,$\frac{sinθ-\sqrt{3}}{2}$),利用坐标运算求出$\overrightarrow{BM}$以及${\overrightarrow{BM}}^{2}$的最大值即可.
解答 解:平面内,|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|=2,$\overrightarrow{DA}$•$\overrightarrow{BC}$=$\overrightarrow{DB}$•$\overrightarrow{AC}$=$\overrightarrow{DC}$•$\overrightarrow{AB}$=0,
∴$\overrightarrow{DA}$⊥$\overrightarrow{BC}$,$\overrightarrow{DB}$⊥$\overrightarrow{AC}$,$\overrightarrow{DC}$⊥$\overrightarrow{AB}$,
可设D(0,0),A(2,0),B(-1,$\sqrt{3}$),C(-1,-$\sqrt{3}$),
∵动点P,M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,
可设P(2+cosθ,sinθ),M($\frac{1+cosθ}{2}$,$\frac{sinθ-\sqrt{3}}{2}$),
∴$\overrightarrow{BM}$=($\frac{3+cosθ}{2}$,$\frac{sinθ-3\sqrt{3}}{2}$),
∴${\overrightarrow{BM}}^{2}$=${(\frac{3+cosθ}{2})}^{2}$+${(\frac{sinθ-3\sqrt{3}}{2})}^{2}$=$\frac{37+12sin(\frac{π}{6}-θ)}{4}$≤$\frac{49}{4}$,
当且仅当sin($\frac{π}{6}$-θ)=1时取等号,
∴|$\overrightarrow{BM}$|2的最大值为$\frac{49}{4}$.
故答案为:$\frac{49}{4}$.
点评 本题考查了平面向量坐标运算性质、模的计算公式、数量积运算性质以及三角函数求值问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
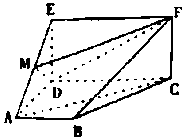 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (0,2) | C. | [0,1] | D. | [-2,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com