
分析 先求出数列的通项,再用数学归纳法进行证明即可.
解答 解:命题“存在正整数n,有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$≥$\frac{7}{4}$”的否定是“对任意的正整数n,有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$<$\frac{7}{4}$”.证明如下:
∵$\frac{2{S}_{n}}{n}$=an+1-$\frac{1}{3}$n2-n-$\frac{2}{3}$,
∴2Sn=nan+1-$\frac{1}{3}$n3-n2-$\frac{2}{3}$n=nan+1-$\frac{1}{3}$n(n+1)(n+2),①
∴当n≥2时,2Sn-1=(n-1)an-$\frac{1}{3}$(n-1)n(n+1),②
由①-②,得2Sn-2Sn-1=nan+1-(n-1)an-n(n+1),
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,∴数列{$\frac{{a}_{n}}{n}$}是以首项为1,公差为1的等差数列.
∴$\frac{{a}_{n}}{n}$=1+1×(n-1)=n,∴an=n2(n≥2),
当n=1时,上式显然成立.∴an=n2,n∈N*.
①当n=1时,$\frac{1}{{a}_{1}}$=1<$\frac{7}{4}$,∴原不等式成立.
②当n≥2时,∵n2>(n-1)•(n+1),
∴$\frac{1}{{n}^{2}}$<$\frac{1}{(n-1)•(n+1)}$=$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),
∴有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$<1+$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$)
=1+$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$)<$\frac{7}{4}$,
∴当n≥2时,∴原不等式亦成立.
综上,对一切正整数n,有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$<$\frac{7}{4}$.
点评 本题考查命题的否定,考查数列的通项,数学归纳法,难度大.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {y|y<0} | B. | {y|y<$\frac{1}{10}$} | C. | {y|0<y<$\frac{1}{10}$} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
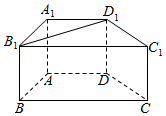 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{p}{2}$,0) | B. | (p,0) | C. | (2p,0) | D. | (3p,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com