
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
分析 要使函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,当且仅当a>0且$\frac{2b}{a}$≤1,即2b≤a,由此利用列举法能求出函数y=f(x)在[1,+∞)上单调递增的概率.
解答 解:∵函数f(x)=ax2-4bx+1的图象的对称轴为x=$\frac{2b}{a}$,
要使函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且$\frac{2b}{a}$≤1,即2b≤a,
若a=1,则b=-2,-1;
若a=2,则b=-2,-1,1;
若a=3,则b=-2,-1,1;
若a=4,则b=-2,-1,1,2;
若a=5,则b=-2,-1,1,2;
∴所求事件包含基本事件的个数是2+3+3+4+4=16,
∴所求事件的概率为$\frac{16}{36}$=$\frac{4}{9}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 3x+2y-6=0 | D. | 2x+3y+6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
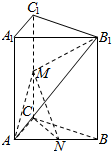 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
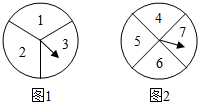 某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.
某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com