
 )的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,0)和(x+2π,-2).
)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,0)和(x+2π,-2).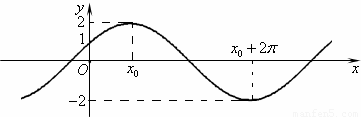
 x+
x+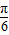 的范围,然后利用正弦函数的值域求f(x)的值域.
的范围,然后利用正弦函数的值域求f(x)的值域.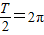 ,T=4π,ω=
,T=4π,ω=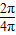 =
= ,
, x+φ),因为f(0)=1=2sinφ,|φ|<
x+φ),因为f(0)=1=2sinφ,|φ|<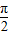 ,所以φ=
,所以φ=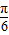 .
. x+
x+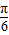 ).
). x+
x+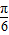 )=2,所以
)=2,所以 x+
x+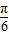 =
=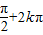 k∈Z,
k∈Z,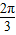 .
.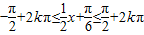 ,k∈Z,
,k∈Z,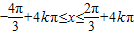 ,k∈Z,
,k∈Z,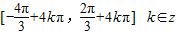 .
. x+
x+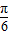
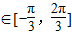 ,∴
,∴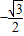 ≤sin(
≤sin( x+
x+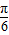 )≤1.
)≤1.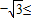 2sin(
2sin( x+
x+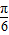 )≤2.
)≤2.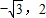 ].
].

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com