
分析 先求出函数f(x)的表达式,通过讨论x的范围结合绝对值的几何意义,从而求出a的范围.
解答 解:∵f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,
∴f(x)=$\left\{\begin{array}{l}{|x-a|-2a,x>0}\\{-|x+a|+2a,x<0}\end{array}\right.$,
又f(x)为R上的“2015型增函数”,
(1)当x>0时,由定义有|x+2015-a|-2a>|x-a|-2a,
即|x+2015-a|>|x-a|,其几何意义为到点a小于到点a-2015的距离,
由于x>0故可知a+a-2015<0得a<$\frac{2015}{2}$
当x<0时,
①若x+2015<0,则有-|x+2015+a|+2a>-|x+a|+2a,
即|x+a|>|x+2015+a|,其几何意义表示到点-a的距离小于到点-a-2015的距离,
由于x<0,故可得-a-a-2015>0,得a<$\frac{2015}{2}$;
②若x+2015>0,则有|x+2015-a|-2a>-|x+a|+2a,
即|x+a|+|x+2015-a|>4a,其几何意义表示到到点-a的距离与到点a-2015的距离的和大于4a,
(2)当a≤0时,显然成立,当a>0时,由于|x+a|+|x+2015+a|≥|-a-a+2015|=|2a-2015|,
故有|2a-2015|>4a,必有2015-2a>4a,解得a<$\frac{2015}{6}$,
综上,对x∈R都成立的实数a的取值范围是 a<$\frac{2015}{6}$,
故答案为:a<$\frac{2015}{6}$.
点评 本题考察了函数的奇偶性,考察新定义问题,根据绝对值的几何意义得到不等式是解答本题的关键,本题是一道中档题.


科目:高中数学 来源: 题型:解答题
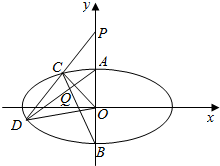 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 32 | C. | 60 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com