
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
分析 求得双曲线C1的离心率,求得双曲线C2一条渐近线方程为y=$\frac{b}{a}$x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.
解答 解:双曲线C1:$\frac{x^2}{16}-\frac{y^2}{4}$=1的离心率为e=$\frac{c′}{a′}$=$\sqrt{1+(\frac{{b}^{′}}{a′})^{2}}$=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,
设F2(c,0),双曲线C2一条渐近线方程为y=$\frac{b}{a}$x,
可得|F2M|=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{bc}{c}$=b,
即有|OM|=$\sqrt{{c}^{2}-{b}^{2}}$=a,
由△OMF2的面积为16,可得$\frac{1}{2}$ab=16,
即ab=32,又a2+b2=c2,且$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,
解得a=8,b=4,c=4$\sqrt{5}$,
即有双曲线的实轴长为16.
故选:C.
点评 本题考查双曲线的方程和性质,注意运用点到直线的距离公式和离心率公式,考查化简整理的运算能力,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
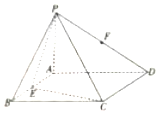 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,且PA=AD=3,$CD=\sqrt{6}$,E、F分别是AB、PD的中点,则点F到平面PCE的距离为( )
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,且PA=AD=3,$CD=\sqrt{6}$,E、F分别是AB、PD的中点,则点F到平面PCE的距离为( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2 | B. | 2ln2 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (0,1) | C. | (0,1] | D. | (-∞,-1)∪(-1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com