
无论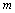 为任何实数,直线
为任何实数,直线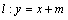 与双曲线
与双曲线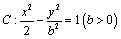 恒有公共点.
恒有公共点.
(1)求双曲线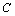 的离心率
的离心率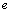 的取值范围;
的取值范围;
(2)若直线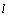 过双曲线
过双曲线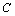 的右焦点
的右焦点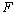 ,与双曲线交于
,与双曲线交于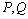 两点,并且满足
两点,并且满足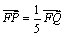 ,求双曲线
,求双曲线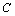 的方程.
的方程.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
已知函数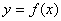 是R上的偶函数,对于
是R上的偶函数,对于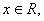 都有
都有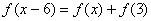 成立,且f(2)=-1,当x1,x2
成立,且f(2)=-1,当x1,x2 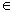 [0,3],且x1≠x2时,都有
[0,3],且x1≠x2时,都有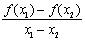 >0.
>0.
则给出下列命题:
① f(2014)=-1; ② 函数y=f(x)图像的一条对称轴为x=6;
③ 函数y=f(x)在[6,9]上为增函数;
④ 函数f(x)在[-12,12]上有8个零点.
其中所有正确命题的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
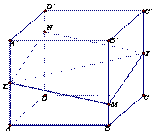
如图所示,正方体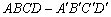 的棱长为1,
的棱长为1, 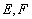 分别是棱
分别是棱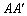 ,
,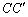 的中点,过直线
的中点,过直线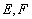 的平面分别与棱
的平面分别与棱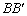 、
、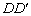 交于
交于 ,设
,设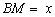 ,
,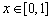 ,给出以下四个命题:
,给出以下四个命题:
①平面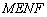
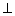 平面
平面 ;
;
②当且仅当x=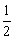 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
③四边形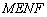 周长
周长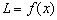 ,
,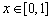 是单调函数;
是单调函数;
④四棱锥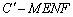 的体积
的体积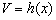 为常函数;
为常函数;
以上命题中假命题的序号为( )
A.①④ B.② C.③ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把△ACD折起,则三棱锥D-ABC的外接球表面积等于 ( )
A.8π B.16π
C.48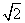 π D.不确定的实数
π D.不确定的实数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com