
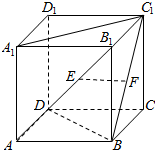
 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)分析 利用构造平行线或平面来进行判断.
解答 解:(1)取BB1中点G,连结EG,FG,
则EG∥AB,FG∥B1C1,
∵BB1⊥AB,BB1⊥B1C1,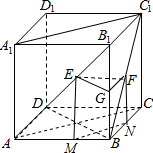
∴BB1⊥EG,BB1⊥FG,又EG∩FG=G,
∴BB1⊥平面EFG,
∵BB1∥CC1,
∴CC1⊥平面EFG,
∴CC1⊥EF.故①正确.
(2)取AB,BC的中点M,N,连结EM,MN,NF,
则EM$\stackrel{∥}{=}$$\frac{1}{2}B{B}_{1}$,FN$\stackrel{∥}{=}$$\frac{1}{2}$CC1$\stackrel{∥}{=}$$\frac{1}{2}$BB1,
∴四边形EMNF是平行四边形,
∴EF∥MN,
∵M,N是AB,BC的中点,
∴MN∥AC,
∴EF∥AC,
∵AC⊥BD,
∴∴BD⊥EF,故②正确.
(3)∵A1C1∥AC,
∴A1C1∥EF,故③错误.
(4)若EF∥AD1,∵EF∥AC,则AD1∥AC,显然不成立,∴EF和AD1不平行.
若EF与AD1相交,则AD1,EF共面,
∵A,D1,F所确定的平面为平面ABC1D1,∴E∈平面ABC1D1,
而A∈平面ABC1D1,∴AB1?平面ABC1D1,显然不成立,∴EF和AD1不相交.
∴EF和AD1异面.
点评 本题考查了空间直线的位置关系判断,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为2π | B. | 函数g(x)为奇函数 | ||
| C. | 函数f(x)在[0.π]递减 | D. | 函数g(x)的最大值为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
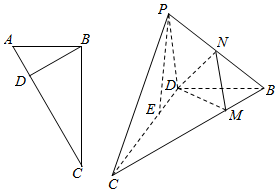 如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.
如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
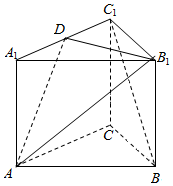 已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.
已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com