
(本小题满分12分)
在边长为2的正方体 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点
(1)求证:CF∥平面
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
(1)根据线面平行的判定定理,结合CF∥OE ,来得到证明。
(2) 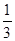
解析试题分析:解:(Ⅰ)取A’D的中点O,连接OF
∵点F为DD’的中点;
∴OF∥A’D’且OF=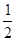 A’D’;
A’D’;
∴OF∥AD且OF=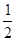 AD; 2分
AD; 2分
∵点E为BC的中点
∴EC∥AD且EC=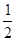 AD;
AD;
∴OF∥EC且OF=EC;
∴四边形OBCF为平行四边形 .3分
∴CF∥OE
又FC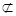 面A’DE且OE
面A’DE且OE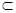 面A’DE
面A’DE
∴CF∥面A’DE .6分
(Ⅱ)取AD的中点M,连接ME
过点M作MH⊥A’D,垂足为H点,连接HE
∵AB∥ME,又AB⊥面ADD’A’
∴ME⊥面ADD’A’
∵A’D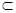 面ADD’A’
面ADD’A’
∴ME⊥A’D
又ME⊥A’D,ME∩MH = M
∴A’D⊥面MHE
∵HE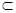 面MHE
面MHE
∴A’D⊥HE
∴∠MHE是二面角E-A’D-A的平面角 .9分
在Rt△MHD中, sin∠A’DA =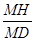
∴MH =" sin" 45°=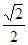
在Rt△MHD中,tan∠MHE =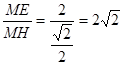
∴sin∠MHE =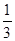 .12分
.12分
考点:空间中点线面的位置关系
点评:解决俄ud关键是对于线面平行的判定定理的运用,以及二面角的求解,属于基础题。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,在三棱锥 中,
中, ,
, ,
, ,
, ,
, , 点
, 点 ,
, 分别在棱
分别在棱 上,且
上,且 ,
,
(Ⅰ)求证: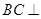 平面PAC
平面PAC
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com