
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(cosB) | C. | f(sinA)>f(sinB) | D. | f(cosA)>f(cosB) |
分析 首先根据A、B是锐角三角形的两个内角,结合y=cosx在区间(0,$\frac{π}{2}$)上是减函数,证出sinA>cosB.然后根据偶函数f(x)满足f(x+1)=-f(x),可得函数f(x)是周期为2的函数,且f(x)在[0,1]上是减函数.最后根据f(x)在[0,1]上是减函数,结合锐角三角形中sinA>cosB,得到f(sinA)<f(cosB).
解答 解:∵A、B是锐角三角形的两个内角,
∴A+B>$\frac{π}{2}$,可得A>$\frac{π}{2}$-B,
∵y=cosx在区间(0,$\frac{π}{2}$)上是减函数,$\frac{π}{2}$>A>$\frac{π}{2}$-B>0,
∴sinA>sin($\frac{π}{2}$-B)=cosB,即锐角三角形的两个内角A、B是满足sinA>cosB,
∵函数f(x)满足f(x+1)=-f(x),
∴f(x+2)=-f(x+1)=-[-f(x)]=f(x),可得函数f(x)是周期为2的函数.
∵f(x)在[-5,-4]上是增函数,
∴f(x)在[-1,0]上也是增函数,
再结合函数f(x)是定义在R上的偶函数,可得f(x)在[0,1]上是减函数.
∵锐角三角形的两个内角A、B是满足sinA>cosB,且sinB、cosA∈[0,1]
∴f(sinA)<f(cosB).
故选:B
点评 本题以函数的单调性与奇偶性为例,考查了锐角三角形的性质、函数的定义域与简单性质等知识点,属于中档题


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{5}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b 不全为0 | B. | a,b全不为0 | ||
| C. | a,b 至少有一个为0 | D. | a不为0且b为0,或 b不为0且a为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},2)$ | B. | (2,+∞) | C. | (1,2) | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | 90 | D. | 180 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
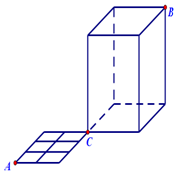 如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.
如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.| A. | 40 | B. | 60 | C. | 80 | D. | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com