
·ÖÎö £¨1£©¸ù¾ÝÌõ¼þ¿ÉÒÔÇó³ö${\overrightarrow{a}}^{2}=4£¬{\overrightarrow{b}}^{2}=1£¬\overrightarrow{a}•\overrightarrow{b}=1$£¬´Ó¶ø½øÐÐÊýÁ¿»ýµÄÔËËã±ã¿ÉÇó³ö$£¨2\overrightarrow{a}-\overrightarrow{b}£©^{2}$µÄÖµ£¬´Ó¶ø¿ÉµÃ³ö$|2\overrightarrow{a}-\overrightarrow{b}|$µÄÖµ£»
£¨2£©ÓÉtan¦È=2£¬¸ù¾ÝÇл¯ÏÒ¹«Ê½¼´¿ÉµÃµ½sin¦È=2cos¦È£¬¶øÓɶþ±¶½ÇµÄÓàÏÒ¹«Ê½¿ÉµÃµ½$2co{s}^{2}\frac{¦È}{2}-1=cos¦È$£¬´Ó¶øÔʽ=$\frac{cos¦È-sin¦È}{sin¦È+cos¦È}$£¬´úÈësin¦È=2cos¦È±ã¿ÉÇó³öÔʽµÄÖµ£®
½â´ð ½â£º£¨1£©¸ù¾ÝÌõ¼þ£¬$£¨2\overrightarrow{a}-\overrightarrow{b}£©^{2}=4{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=16-4+1=13£»
¡à$|2\overrightarrow{a}-\overrightarrow{b}|=\sqrt{13}$£»
£¨2£©tan¦È=2£»
¡à$\frac{sin¦È}{cos¦È}=2$£»
¡àsin¦È=2cos¦È£»
¡à$\frac{2co{s}^{2}\frac{¦È}{2}-sin¦È-1}{sin¦È+cos¦È}=\frac{cos¦È-sin¦È}{sin¦È+cos¦È}$
=$\frac{cos¦È-2cos¦È}{2cos¦È+cos¦È}$
=$-\frac{1}{3}$£®
µãÆÀ ¿¼²éÏòÁ¿ÊýÁ¿»ýµÄÔËËã¼°¼ÆË㹫ʽ£¬ÒªÇó$|2\overrightarrow{a}-\overrightarrow{b}|$¶øÇó$£¨2\overrightarrow{a}-\overrightarrow{b}£©^{2}$µÄ·½·¨£¬ÒÔ¼°Çл¯ÏÒ¹«Ê½£¬¶þ±¶½ÇµÄÓàÏÒ¹«Ê½£®


 ÔÆÄÏʦ´ó¸½Ð¡Ò»ÏßÃûʦÌáÓÅ×÷ҵϵÁдð°¸
ÔÆÄÏʦ´ó¸½Ð¡Ò»ÏßÃûʦÌáÓÅ×÷ҵϵÁдð°¸ ³å´Ì100·Öµ¥ÔªÓÅ»¯Á·¿¼¾íϵÁдð°¸
³å´Ì100·Öµ¥ÔªÓÅ»¯Á·¿¼¾íϵÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
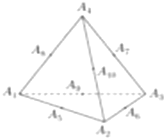 ÒÑÖªÕýËÄÃæÌåA1A2A3A4£¬µãA5£¬A6£¬A7£¬A8£¬A9£¬A10·Ö±ðÊÇËùÔÚÀâµÄÖе㣬Èçͼ£¬Ôòµ±1¡Üi¡Ü10£¬1¡Üj¡Ü10£¬ÇÒi¡Ùjʱ£¬ÊýÁ¿»ý$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$µÄ²»Í¬ÊýÖµµÄ¸öÊýΪ9£®
ÒÑÖªÕýËÄÃæÌåA1A2A3A4£¬µãA5£¬A6£¬A7£¬A8£¬A9£¬A10·Ö±ðÊÇËùÔÚÀâµÄÖе㣬Èçͼ£¬Ôòµ±1¡Üi¡Ü10£¬1¡Üj¡Ü10£¬ÇÒi¡Ùjʱ£¬ÊýÁ¿»ý$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$µÄ²»Í¬ÊýÖµµÄ¸öÊýΪ9£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | $-\frac{{\sqrt{3}}}{2}$ | B£® | $-\frac{1}{2}$ | C£® | $\frac{{\sqrt{3}}}{2}$ | D£® | $\frac{1}{2}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | £¨$\frac{2}{3}$£¬1£© | B£® | £¨2£¬+¡Þ£© | C£® | £¨$\frac{2}{3}$£¬1£©¡È£¨1£¬+¡Þ£© | D£® | £¨0£¬$\frac{2}{3}$£©¡È£¨1£¬+¡Þ£© |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com