
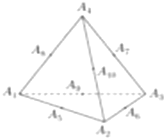
 已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.
已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9. 分析 设出已知正四面体的棱长,求出四个面上的每一个顶点与对边中点的连线长,每一对相对棱的中点连线得长,然后分别求i=1,j自1取到10,所得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值,同理求得i=2,j自1取到10,所得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值,…i=10,j自1取到10,所得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值,比较结果后得答案.
解答 解: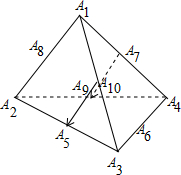 ∵四面体A1A2A3A4是正四面体,
∵四面体A1A2A3A4是正四面体,
∴四面体的所有棱长相等,设为a,四个面上的每一个顶点与对边中点的连线长均为$\frac{\sqrt{3}}{2}a$,
每一对相对棱的中点连线相等均为$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}-(\frac{1}{2}a)^{2}}=\frac{\sqrt{2}}{2}a$.
当i=1,j自1取到10,所得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值有:
$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{2}}$=a2,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{3}}=\frac{1}{2}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{4}}=\frac{1}{2}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{5}}=\frac{3}{4}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{6}}=\frac{1}{2}{a}^{2}$,
$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{7}}=\frac{1}{4}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{8}}=\frac{1}{2}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{9}}=\frac{3}{4}{a}^{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{10}}=\frac{1}{4}{a}^{2}$.
当i=2,j自1取到10时,依次求得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值,
…
i=10,j自1取到10,依次求得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值,
比较结果后得数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值有$-{a}^{2},-\frac{3}{4}{a}^{2},-\frac{1}{2}{a}^{2},-\frac{1}{4}{a}^{2}$,0,$\frac{1}{4}{a}^{2},\frac{1}{2}{a}^{2},\frac{3}{4}{a}^{2},{a}^{2}$共9个.
故答案为:9.
点评 本题考查向量在几何体中的应用,考查了平面向量的数量积运算,考查空间想象能力和思维能力,属中档题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com