练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．执行如图所示的程序框，输出的T=（　　）
    A．17B．29C．44D．52

    分析 模拟执行程序框图，依次写出每次循环得到的S，n，T的值，当S=12，T=29时满足条件T＞2S，退出循环，输出T的值为29．

    解答 解：模拟执行程序框图，可得
    S=3，n=1，T=2
    不满足条件T＞2S，S=6，n=2，T=8
    不满足条件T＞2S，S=9，n=3，T=17
    不满足条件T＞2S，S=12，n=4，T=29
    满足条件T＞2S，退出循环，输出T的值为29．
    故选：B．

    点评 本题主要考查了循环结构的程序框图，依次写出每次循环得到的S，n，T的值是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=（a-x）ex-1（e为自然对数的底数）．
    （Ⅰ）当a=1时，求f（x）的最大值；
    （Ⅱ）当x∈（-∞，0）∪（0，+∞）时，$\frac{f（x）}{x}$＜1恒成立，证明：a=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知在△ABC中，∠A、∠B、∠C所对的边是a、b、c，$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$且$\overrightarrow{GA}$•$\overrightarrow{GB}$=0，若（tanA+tanB）•tanC=mtanAtanB，则m的值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数f（x）=|sinx|，x∈[-2π，2π]，则方程f（x）=$\frac{1}{2}$的所有根的和等于（　　）
    A．0B．πC．-πD．-2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

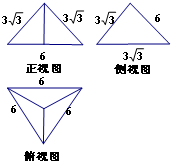    11．正四面体（即各条棱长均相等的三棱锥）的棱长为6，某学生画出该正四面体的三视图如下，其中有一个视图是错误的，则该视图修改正确后对应图形的面积为6$\sqrt{6}$．该正四面体的体积为18$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

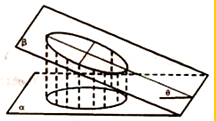    1．如图，一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截，其截面是一个椭圆Γ，以该椭圆Γ的中心为原点，长轴所在的直线
    为x轴，建立平面直角坐标系．点F是椭圆的右焦点．点M（m，0）、N（0，n）分别是x轴、y轴上的动点，且满足$\overrightarrow{MN}$•$\overrightarrow{NF}$=0，若点P满足$\overrightarrow{OM}$=
    2$\overrightarrow{ON}$+$\overrightarrow{PO}$．
    （1）求该椭圆Γ的长轴长及点P的轨迹C的方程；
    （2）设过点F任作一直线与点P的轨迹交于A、B两点，直线OA、OB与直线x=-1分别交于点S、T（O为坐标原点），试判断$\overrightarrow{FS}$•$\overrightarrow{FT}$是否为定值？若是．求出这个定值：若不是．请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=mlnx+$\frac{2m}{x}$-$\frac{{e}^{x}}{{x}^{2}}$
    （1）若m≤0，求函数f（x）的单调区间；
    （2）若函数f（x）在（0，2）内存在两个极值点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的离心率为$\frac{\sqrt{2}}{2}$，点Q（$\frac{\sqrt{2}}{2}，\frac{\sqrt{3}}{2}$）在椭圆C上．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设P为椭圆C上异于其顶点的动点，O为坐标原点，过椭圆右焦点F2作OP平行线交椭圆C于A、B两点．
    （i）试探究|OP|2和|AB|的比值是否为一个常数？若是，求出这个常数，若不是，请说明理由．
    （ii）记△PF2A的面积为S1，△OF2B的面积为S2，令S=S1+S2，求证：S$＜\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若变量x，y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤4\\ y≥k\end{array}$且z=2x+y的最小值为-3，则k=-1．

    查看答案和解析>>

    同步练习册答案