
【题目】已知![]() 是椭圆
是椭圆![]() (
(![]() )的左顶点,左焦点
)的左顶点,左焦点![]() 是线段
是线段![]() 的中点,抛物线
的中点,抛物线![]() 的准线恰好过点
的准线恰好过点![]() .
.
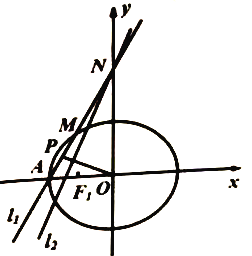
(1)求椭圆的方程;
(2)如图所示,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆于点
交椭圆于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 为线段
为线段![]() 的中点,过
的中点,过![]() 作与直线
作与直线![]() 垂直的直线
垂直的直线![]() ,证明对于任意的
,证明对于任意的![]() (
(![]() ),直线
),直线![]() 过定点,并求出此定点坐标.
过定点,并求出此定点坐标.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点M(﹣2,﹣1),离心率为
经过点M(﹣2,﹣1),离心率为![]() .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(Ⅰ)求椭圆C的方程;
(Ⅱ)试判断直线PQ的斜率是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与
与![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,与直线
,与直线![]() 相交于
相交于![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 均不重合).证明:
均不重合).证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数![]() 随时刻
随时刻![]() (时)变化的规律满足表达式
(时)变化的规律满足表达式![]() ,
,![]() ,其中
,其中![]() 为空气治理调节参数,且
为空气治理调节参数,且![]() .
.
(1)令![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若规定每天中![]() 的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数
的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800 名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
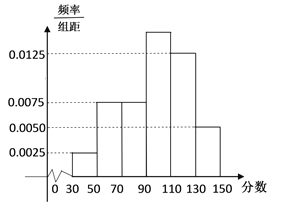
(Ⅰ)求初赛分数在区间![]() 内的频率;
内的频率;
(Ⅱ)求获得复赛资格的人数;
(Ⅲ)据此直方图估算学生初赛成绩的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线l:(m+3)x-(m+2)y+m=0与圆C:(x-3)2+(y-4)2=9.
(1)求证:无论m为何值,直线l总过定点A,并说明直线l与圆C总相交.
(2)m为何值时,直线l被圆C所截得的弦长最小?请求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
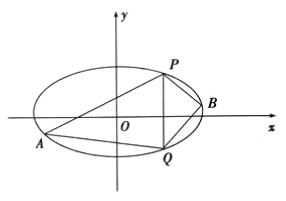
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com