
分析 已知$\sqrt{2\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,$\sqrt{3\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,$\sqrt{4\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,…,照此规律,第5个等式中:a=6,t=a2-1=35,可得结论.
解答 解:已知$\sqrt{2\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,$\sqrt{3\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,$\sqrt{4\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,…,照此规律,第5个等式中:a=6,t=a2-1=35,
故答案为:6,35.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
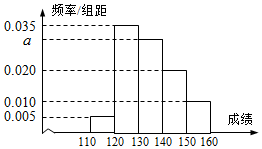 从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.
从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -α | B. | α+$\frac{π}{2}$ | C. | α+π | D. | $\frac{π}{2}$-α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
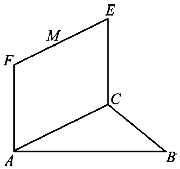 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com