
若数列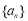 的各项均为正数,
的各项均为正数,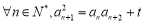 ,
,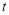 为常数,且
为常数,且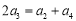 .
.
(1)求 的值;
的值;
(2)证明:数列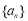 为等差数列;
为等差数列;
(3)若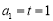 ,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使
,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使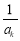 ,
,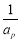 ,
,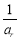 成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
(1)2(2)详见解析(3)当k=1时,不存在p,r;当k≥2时,存在一组p=2k-1,r=k(2k-1)满足题意.
【解析】
试题分析:(1)令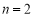 ,得
,得 ①,令
①,令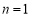 ,得
,得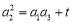 ②,①—②,得
②,①—②,得  ,
,  ,
,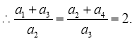 (2)证明数列为等差数列,一般利用定义进行证明,由(1)推导过程知:
(2)证明数列为等差数列,一般利用定义进行证明,由(1)推导过程知: ,
, 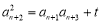 ,两式相减得
,两式相减得 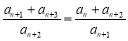
 数列
数列 为常数数列,
为常数数列,
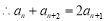 ,
,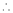 数列
数列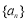 为等差数列(3)先求数列
为等差数列(3)先求数列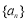 通项公式:由(2)知,数列
通项公式:由(2)知,数列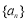 为等差数列,设公差为
为等差数列,设公差为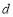 ,则由条件
,则由条件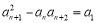 ,得
,得
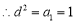 ,又数列
,又数列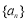 的各项为正数,
的各项为正数, ,
, ,
,
若存在p,r使 ,
,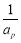 ,
,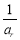 成等差数列,则
成等差数列,则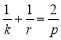 所以
所以 ;当k=1时,
;当k=1时, ,舍去;当k≥2时,令p=2k-1得r=kp=k(2k-1),满足k<p<r.
,舍去;当k≥2时,令p=2k-1得r=kp=k(2k-1),满足k<p<r.
试题解析:【解析】
(1)由条件,设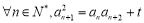
令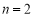 ,得
,得 ①,令
①,令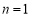 ,得
,得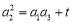 ②
②
①—②,得  ,
,  ,
,
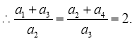 4分
4分
(2) ,
, 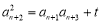 ,
,
两式相减得 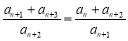 7分
7分
 数列
数列 为常数数列,
为常数数列,
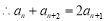 ,
, 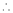 数列
数列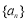 为等差数列. 10分
为等差数列. 10分
(3)由(2)知,数列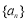 为等差数列,设公差为
为等差数列,设公差为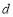 ,
,
则由条件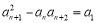 ,得
,得
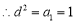 ,又数列
,又数列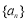 的各项为正数,
的各项为正数,
 ,
, ,
, . 12分
. 12分
当k=1时,若存在p,r使 ,
,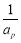 ,
,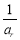 成等差数列,则
成等差数列,则
与 矛盾.因此,当k=1时,不存在. 14分
矛盾.因此,当k=1时,不存在. 14分
当k≥2时,则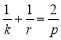 所以
所以
令p=2k-1得r=kp=k(2k-1),满足k<p<r.
综上所述,当k=1时,不存在p,r;
当k≥2时,存在一组p=2k-1,r=k(2k-1)满足题意. 16分
考点:等差数列


科目:高中数学 来源:2014-2015学年广东省揭阳市高一上学期期中考试数学试卷(解析版) 题型:选择题
设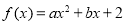 是定义在
是定义在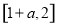 上的偶函数,则
上的偶函数,则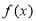 的值域是( ).
的值域是( ).
A. B.
B.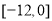 C.
C.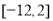 D.与
D.与 有关,不能确定
有关,不能确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省揭阳市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
—个几何体的三视图及其尺寸如右图所示,则该几何体的表面积为( )

A.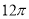 B.
B. C.
C. D.
D.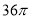
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考文科数学试卷(解析版) 题型:解答题
已知函数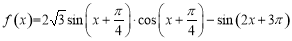 .
.
(1)求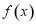 的最小正周期;
的最小正周期;
(2)若将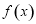 的图像向左平移
的图像向左平移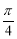 个单位,得到函数
个单位,得到函数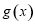 的图像,
的图像,
求函数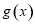 在区间
在区间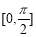 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考文科数学试卷(解析版) 题型:填空题
设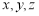 是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若 ,且
,且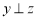 ,则
,则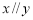 ”为真命题的是 . (填所正确条件的代号)
”为真命题的是 . (填所正确条件的代号)
①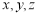 为直线;
为直线;
② 为平面;
为平面;
③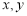 为直线,
为直线,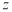 为平面;
为平面;
④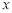 为直线,
为直线,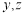 为平面.
为平面.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考理科数学试卷(解析版) 题型:解答题
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈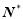 )名员工从事第三产业,调整后他们平均每人每年创造利润为
)名员工从事第三产业,调整后他们平均每人每年创造利润为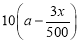 万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:解答题
(本题满分16分)已知数列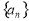 中
中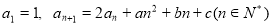 .
.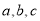 为实常数.
为实常数.
(Ⅰ)若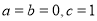 ,求数列
,求数列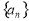 的通项公式;
的通项公式;
(Ⅱ)若 .①是否存在常数
.①是否存在常数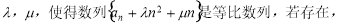 求出
求出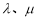 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②设  .证明:n≥2时,
.证明:n≥2时, 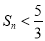 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com