
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
分析 根据向量模长公式求出满足条件的k的个数,再根据古典概型的计算公式进行求解.
解答 解:∵$|{\overrightarrow{AB}}|≤4$∴$\sqrt{{k}^{2}+1}≤4$∴$-\sqrt{15}≤k≤\sqrt{15}$
又∵k为整数,则k∈{-3,-2,-1,0,1,2,3}
若△ABC为直角三角形,则
当A为直角时,$\overrightarrow{AB}•\overrightarrow{AC}=2k+4=0$,即k=-2
当B为直角时,$|\overrightarrow{AC}{|}^{2}={|\overrightarrow{AB}|}^{2}+{|\overrightarrow{BC}|}^{2}$,即k=-1或k=3
∵$|{\overrightarrow{AB}}|≤4$,
∴C不可能为直角.
故△ABC是直角三角形的概率P=$\frac{3}{7}$,
故选:C.
点评 本题主要考查概率的计算,根据古典概型的概率公式,利用列举法进行求解是解决本题的关键.


科目:高中数学 来源: 题型:解答题
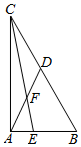 已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$
已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|0<a<1} | B. | $\left\{{\left.a\right|1<a<\sqrt{2}}\right\}$ | ||
| C. | $\left\{{\left.a\right|-\sqrt{2}<a<-1}\right.$或$\left.{1<a<\sqrt{2}}\right\}$ | D. | $\left\{{\left.a\right|-\sqrt{2}<a<\sqrt{2}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com