
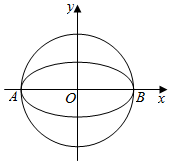
 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.分析 (Ⅰ)椭圆W的左顶点A在圆O:x2+y2=16上求得a,结合离心率求得c,再由隐含条件求得b,则椭圆方程可求;
(Ⅱ)法一:(i)设直线方程为y=k(x+4),联立直线方程和椭圆方程,化为关于x的一元二次方程,利用弦长公式列式求得k值;
(ii)由点到直线的距离公式求出圆心到直线AP的距离,再由垂径定理求得|AQ|,代入$\frac{|PQ|}{|AP|}=\frac{|AQ|-|AP|}{|AP|}=\frac{|AQ|}{|AP|}-1$,可得满足条件的直线AP不存在;
法二:(i)直线AP的方程为x=my-4,联立直线方程和椭圆方程,化为关于y的一元二次方程,利用弦长公式列式求得k值;
(ii)由点到直线的距离公式求出圆心到直线AP的距离,再由垂径定理求得|AQ|,代入$\frac{|PQ|}{|AP|}=\frac{|AQ|-|AP|}{|AP|}=\frac{|AQ|}{|AP|}-1$,可得满足条件的直线AP不存在.
解答 解:(Ⅰ)∵椭圆W的左顶点A在圆O:x2+y2=16上,∴a=4.
又离心率为$\frac{{\sqrt{3}}}{2}$,∴$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,则$c=2\sqrt{3}$,
∴b2=a2-c2=4,
∴W的方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$;
(Ⅱ)法一:(i)设点P(x1,y1),Q(x2,y2),显然直线AP存在斜率,
设直线AP的方程为y=k(x+4),
与椭圆方程联立得$\left\{\begin{array}{l}y=k(x+4)\\ \frac{x^2}{16}+\frac{y^2}{4}=1\end{array}\right.$,
化简得到(1+4k2)x2+32k2x+64k2-16=0,
∵-4为上面方程的一个根,∴${x_1}+(-4)=\frac{{-32{k^2}}}{{1+4{k^2}}}$,则${x_1}=\frac{{4-16{k^2}}}{{1+4{k^2}}}$.
由$|AP|=\sqrt{1+{k^2}}|{x_1}-(-4)|=\frac{{8\sqrt{2}}}{5}$,
代入得到$|AP|=\frac{{8\sqrt{1+{k^2}}}}{{1+4{k^2}}}=\frac{{8\sqrt{2}}}{5}$,解得k=±1,
∴直线AP的斜率为1,-1;
(ii)∵圆心到直线AP的距离为$d=\frac{|4k|}{{\sqrt{{k^2}+1}}}$,
∴$|AQ|=2\sqrt{16-{d^2}}=2\sqrt{\frac{16}{{1+{k^2}}}}=\frac{8}{{\sqrt{1+{k^2}}}}$.
∵$\frac{|PQ|}{|AP|}=\frac{|AQ|-|AP|}{|AP|}=\frac{|AQ|}{|AP|}-1$,
代入得到$\frac{|PQ|}{|AP|}=\frac{{\frac{8}{{\sqrt{1+{k^2}}}}}}{{\frac{{8\sqrt{1+{k^2}}}}{{1+4{k^2}}}}}-1=\frac{{1+4{k^2}}}{{1+{k^2}}}-1=\frac{{3{k^2}}}{{1+{k^2}}}=3-\frac{3}{{1+{k^2}}}$.
显然$3-\frac{3}{{1+{k^2}}}≠3$,
∴不存在直线AP,使得$\frac{|PQ|}{|AP|}=3$.
法二:(i)设点P(x1,y1),Q(x2,y2),显然直线AP存在斜率且不为0,
设直线AP的方程为x=my-4,
与椭圆方程联立得$\left\{\begin{array}{l}x=my-4\\ \frac{x^2}{16}+\frac{y^2}{4}=1\end{array}\right.$,
化简得到(m2+4)y2-8my=0,
显然-4上面方程的一个根,∴另一个根,即${y_1}=\frac{8m}{{{m^2}+4}}$,
由$|AP|=\sqrt{1+{m^2}}|{y_1}-0|=\frac{{8\sqrt{2}}}{5}$,
代入得到$|AP|=\sqrt{1+{m^2}}\frac{8|m|}{{{m^2}+4}}=\frac{{8\sqrt{2}}}{5}$,解得m=±1.
∴直线AP的斜率为1,-1;
(ii)∵圆心到直线AP的距离为$d=\frac{|4|}{{\sqrt{1+{m^2}}}}$,
∴$|AQ|=2\sqrt{16-{d^2}}=2\sqrt{\frac{{16{m^2}}}{{1+{m^2}}}}=\frac{8|m|}{{\sqrt{1+{m^2}}}}$.
∵$\frac{|PQ|}{|AP|}=\frac{|AQ|-|AP|}{|AP|}=\frac{|AQ|}{|AP|}-1$,
代入得到$\frac{|PQ|}{|AP|}=\frac{{\frac{8|m|}{{\sqrt{1+{m^2}}}}}}{{\sqrt{1+{m^2}}\frac{8|m|}{{{m^2}+4}}}}-1=\frac{{{m^2}+4}}{{1+{m^2}}}-1=\frac{3}{{1+{m^2}}}$.
若$\frac{3}{{1+{m^2}}}=3$,则m=0,与直线AP存在斜率矛盾,
∴不存在直线AP,使得$\frac{|PQ|}{|AP|}=3$.
点评 本题考查椭圆方程的求法,考查了直线和圆锥曲线位置关系的应用,训练了弦长公式的应用,考查点到直线距离公式,属中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
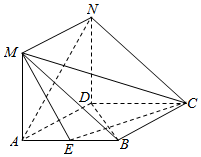 在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com