
| A. | ($\frac{1}{4}$,$\frac{5}{4}$]∪($\frac{7}{4}$,+∞) | B. | ($\frac{1}{4}$,$\frac{7}{4}$) | C. | (-∞,$\frac{1}{4}$]∪[$\frac{5}{4}$,+∞) | D. | ($\frac{1}{4}$,$\frac{5}{4}$]∪[$\frac{7}{4}$,+∞) |
分析 利用已知条件列出方程求出a,b,然后利用分段函数分别求解函数的值域即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{(lnx)^{2}+alnx+b,x>0}\\{{e}^{x}+\frac{1}{4},x≤0}\end{array}\right.$,且f(e)=f(1),f(e2)=f(0)+$\frac{11}{4}$,
可得:$\left\{\begin{array}{l}{1+a+b=b}\\{4+2a+b=4}\end{array}\right.$,解得a=-1,b=2,
所以当x>0时,f(x)=(lnx)2-lnx+2=(lnx-$\frac{1}{2}$)2+$\frac{7}{4}$$≥\frac{7}{4}$,
当x≤0时,可得$\frac{1}{4}<{e}^{x}+\frac{1}{4}≤{e}^{0}+\frac{1}{4}$=$\frac{5}{4}$,
则函数f(x)的值域为($\frac{1}{4}$,$\frac{5}{4}$]∪[$\frac{7}{4}$,+∞).
故选:D.
点评 本题考查分段函数的应用,函数的值域的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
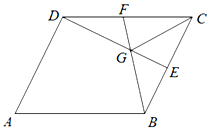 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 119 | C. | 114 | D. | 110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com