
| �� | A��� | B��� | C��� |
| ��һ�ְָ� | ������2 | ��������1 | ����������1 |
| �ڶ��ְָ� | ������1 | ��������3 | ����������1 |
���� ���⿼���֪ʶ���Ǽ����Թ滮��Ӧ�ã�������֪�����н⣺���õ�һ�ְָ�x�ţ��ڶ��ְָ�y�ţ������A�ֵ�Ϊ2x+y����B�ֵ�Ϊx+3y����C�ֵ�Ϊx+y��������ó�Լ��������Ŀ�꺯����Ȼ���������Թ滮��������Ž⣮
��� �⣺��1������ص�һ�ְָ�x�ţ��ڶ��ְָ�y�ţ����øְ���Ϊz��
����$\left\{\begin{array}{l}{2x+y��15}\\{x+3y��27}\\{x+y��13}\\{x��0}\\{y��0}\end{array}\right.$��������������ͼ����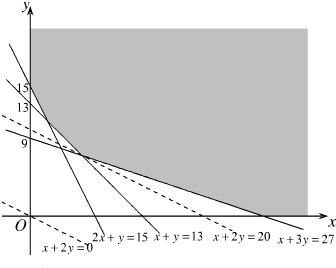 ��
��
��2�������øְ�������zm2��Ŀ�꺯��Ϊz=x+2y��
��y=-$\frac{1}{2}$x+$\frac{1}{2}$z��
��$\left\{\begin{array}{l}{x+3y=27}\\{x+y=13}\end{array}\right.$ ��M��6��7����
���ͼ���z����Сֵ��6+2��7=20��
������������������£��õ�һ�ְָ�6�ţ��ڶ��ְָ�7�ţ����øְ������С��
���� �ڽ�����Թ滮��Ӧ����ʱ���䲽��Ϊ���ٷ�����Ŀ��������Ĺ�ϵ���г�����ʽ�飬��Լ������⇒����Լ����������������⇒�۷���Ŀ�꺯��Z��ֱ�߽ؾ�֮��Ĺ�ϵ⇒��ʹ��ƽ��ֱ�߷�������Ž�⇒�ݻ�ԭ����ʵ�����У�


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com