
分析 由已知得y=$\frac{4{k}^{2}}{1-{k}^{2}}$=k×$\frac{4k}{1-{k}^{2}}$=kx,从而k=$\frac{y}{x}$,由此能求出该参数方程的普通方程.
解答 解:∵参数方程$\left\{\begin{array}{l}{x=\frac{4k}{1-{k}^{2}}}\\{y=\frac{4{k}^{2}}{1-{k}^{2}}}\end{array}\right.$(k为参数),
∴y=$\frac{4{k}^{2}}{1-{k}^{2}}$=k×$\frac{4k}{1-{k}^{2}}$=kx,
∴该参数方程的普通方程为y=kx,∴k=$\frac{y}{x}$,
∴x=$\frac{4×\frac{y}{x}}{1-\frac{{y}^{2}}{{x}^{2}}}$,整理,得该曲线的普通方程为x2-y2-4y=0.
它表示焦点在y轴上的双曲线.
点评 本题考查曲线的普通方程的求法,考查直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
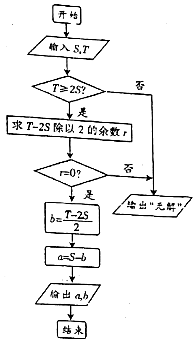
| A. | 17,23 | B. | 21,21 | C. | 19,23 | D. | 20,20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com