
| AΘ° | 0 | BΘ° | 6$\sqrt{2}$ | CΘ° | 36 | DΘ° | 72 |
Ζ÷Έω ÷±Ϋ”άϊ”ΟœρΝΩΒΡΡΘ«σΖ®“‘ΦΑœρΝΩΒΡ ΐΝΩΜΐ«σΫβΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$¬ζΉψ$\overrightarrow{a}$•$\overrightarrow{b}$=0Θ§|$\overrightarrow{a}$|=2Θ§|$\overrightarrow{b}$|=3Θ§‘ρ|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{9{\overrightarrow{a}}^{2}-12\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}$=$\sqrt{36+36}$=$6\sqrt{2}$Θ°
Ι ―ΓΘΚBΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΤΫΟφœρΝΩΒΡ ΐΝΩΜΐ“‘ΦΑœρΝΩΒΡΡΘΒΡ«σΖ®Θ§ΩΦ≤ιΦΤΥψΡήΝΠΘ°


 Ή÷¥ ΨδΕΈΤΣœΒΝ–¥πΑΗ
Ή÷¥ ΨδΕΈΤΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{1-\sqrt{3}}{2}$+$\frac{1+\sqrt{3}}{2}$i | BΘ° | $\frac{1-\sqrt{3}}{2}$-$\frac{1+\sqrt{3}}{2}$i | CΘ° | $\frac{1+\sqrt{3}}{2}$+$\frac{1-\sqrt{3}}{2}$i | DΘ° | $\frac{1+\sqrt{3}}{2}$-$\frac{1-\sqrt{3}}{2}$i |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
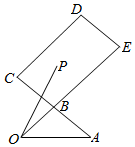 »γΆΦΘ§B «ACΒΡ÷–ΒψΘ§$\overrightarrow{BE}$=2$\overrightarrow{OB}$Θ§P «ΨΊ–ΈBCDEΡΎΘ®Κ§±ΏΫγΘ©ΒΡ“ΜΒψΘ§«“$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$Θ®xΘ§yΓ RΘ©Θ°‘ρx-yΒΡΉν¥σ÷ΒΈΣ-1Θ°
»γΆΦΘ§B «ACΒΡ÷–ΒψΘ§$\overrightarrow{BE}$=2$\overrightarrow{OB}$Θ§P «ΨΊ–ΈBCDEΡΎΘ®Κ§±ΏΫγΘ©ΒΡ“ΜΒψΘ§«“$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$Θ®xΘ§yΓ RΘ©Θ°‘ρx-yΒΡΉν¥σ÷ΒΈΣ-1Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{2}$ | BΘ° | 1 | CΘ° | $\frac{\sqrt{2}}{2}$ | DΘ° | $\frac{1}{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com