
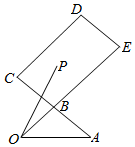
 如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1.
如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1. 分析 可分别过P作PM∥AO,PN∥OE,从而得到平行四边形PMON,从而有$\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{OM}$,而$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,从而根据图形便可得到x≤0,y≥1,这样便得出x=0,y=1时,x-y取到最大值-1.
解答 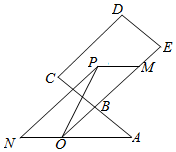 解:如图,过P作PM∥AO,交OE于M,作PN∥OE,交AO的延长线于N,则:
解:如图,过P作PM∥AO,交OE于M,作PN∥OE,交AO的延长线于N,则:
$\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{OM}$;
又$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$;
∴x≤0,y≥1;
由图形看出,当P与B重合时:$\overrightarrow{OP}=0•\overrightarrow{OA}+1•\overrightarrow{OB}$;
此时x取最大值0,y取最小值1;
∴此时x-y取最大值-1;
即x-y的最大值为-1.
故答案为:-1.
点评 考查向量加法的平行四边形法则,平面向量基本定理,向量数乘的几何意义,以及数形结合解题的方法.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{5}}{5}$,+∞) | B. | [$\sqrt{2}$,+∞) | C. | [$\frac{\sqrt{5}}{5}$,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4} | B. | {0,2,4} | C. | {2,4} | D. | {3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 输出使1×2×4×…×n≥2015成立的最小整数n | |
| B. | 输出使1×2×4×…×n≥2015成立的最大整数n | |
| C. | 输出使1×2×4×…×n≥2015成立的最大整数n+2 | |
| D. | 输出使1×2×4×…×n≥2015成立的最小整数n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三个函数的单调性总相同 | |
| B. | 当1<a<2时,对任意x>0,f(x)>g(x)>h(x) | |
| C. | 当a>1时,三个函数没有公共点 | |
| D. | 任意a>1,三个函数都与直线y=x相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 6$\sqrt{2}$ | C. | 36 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=lg$\frac{x-1}{x+1}$ | B. | f(x)=ex-$\frac{1}{{e}^{x}}$ | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=x2-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com