

| A. | f(x)=lg$\frac{x-1}{x+1}$ | B. | f(x)=ex-$\frac{1}{{e}^{x}}$ | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=x2-4 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)存在零点,②f(x)+f(-x)=0,即函数f(x)为奇函数,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
解答 解:模拟执行程序,可知该程序的作用是输出满足条件①f(x)存在零点,②f(x)+f(-x)=0的函数f(x),
即函数f(x)为奇函数,即函数图象与x轴有交点.
由于:A:f(x)=lg$\frac{x-1}{x+1}$、C:f(x)=$\frac{1}{{x}^{3}}$,D、f(x)=x2-4不是奇函数,故不满足条件②f(x)+f(-x)=0,
而B:f(x)=ex-$\frac{1}{{e}^{x}}$既是奇函数,而且函数图象与x也有交点,
故B:f(x)=ex-$\frac{1}{{e}^{x}}$符合输出的条件.
故选:B.
点评 本题主要考查程序框图的识别和应用,根据程序满足的条件是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
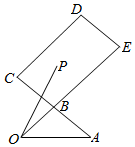 如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1.
如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{2}$+2 | B. | $\frac{5\sqrt{2}}{2}$+1 | C. | $\frac{5\sqrt{2}}{2}$-2 | D. | $\frac{5\sqrt{2}}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com