Question

9．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-4y²=1（a＞0）的右顶点到其一条渐近线的距离等于$\frac{\sqrt{3}}{4}$，抛物线E：y²=2px的焦点与双曲线C的右焦点重合，直线l的方程为x-y+4=0，在抛物线上有一动点M到y轴的距离为d₁，到直线l的距离为d₂，则d₁+d₂的最小值为（　　）

• A． $\frac{5\sqrt{2}}{2}$+2
• B． $\frac{5\sqrt{2}}{2}$+1
• C． $\frac{5\sqrt{2}}{2}$-2
• D． $\frac{5\sqrt{2}}{2}$-1

Answer 1

分析 求出双曲线的渐近线方程，运用点到直线的距离公式计算可得a，进而得到c，由抛物线的焦点坐标，可得p=2，进而得到抛物线的方程．连接MF，过点M作MA⊥l于点A，作MB⊥y轴于点B，MB的延长线交准线x=-1于点C．由抛物线的定义，得到d₁+d₂=（MA+MF）-1，再由平面几何知识可得当M、A、F三点共线时，MA+MF有最小值，因此算出F到直线l的距离，即可得到d₁+d₂的最小值．

解答 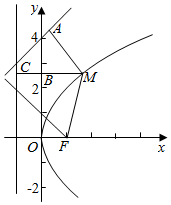解：双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-4y²=1的渐近线方程为y=±$\frac{x}{2a}$，
右顶点（a，0）到其一条渐近线的距离等于$\frac{\sqrt{3}}{4}$，可得
$\frac{a}{\sqrt{1+4{a}^{2}}}$=$\frac{\sqrt{3}}{4}$，解得a=$\frac{\sqrt{3}}{4}$，
即有c=$\sqrt{{a}^{2}+{b}^{2}}$=1，
由题意可得$\frac{p}{2}$=1，解得p=2，
即有抛物线的方程为y²=4x，
如图，过点M作MA⊥l于点A，
作MB⊥y轴于点B，MB的延长线交准线x=-1于点C
连接MF，根据抛物线的定义得MA+MC=MA+MF
∵M到y轴的距离为d₁，M到直线l的距离为d₂，
∴d₁+d₂=MA+MB=（MA+MC）-1=（MA+MF）-1
根据平面几何知识，可得当M、A、F三点共线时，MA+MF有最小值．
∵F（1，0）到直线l：x-y+4=0的距离为$\frac{|1-0+4|}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$，
∴MA+MF的最小值是$\frac{5\sqrt{2}}{2}$，
由此可得d₁+d₂的最小值为$\frac{5\sqrt{2}}{2}$-1．
故选：D．

点评 本题考查双曲线的方程和性质，主要是渐近线方程的运用，同时考查抛物线的方程和性质，给出抛物线和直线l，求抛物线上一点到y轴距离与直线l距离之和的最小值，着重考查了点到直线的距离公式、抛物线的定义和简单几何性质等知识，属于中档题．