
 在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.
在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.分析 (1)证明AB⊥面ACC1A1,即有AB⊥CD;又AC=A1C,D为AA1中点,则CD⊥AA1.即可证明:CD⊥平面AB1;
(2)求出平面的法向量,利用二面角E-A1C1-A的大小为$\frac{π}{3}$,即可得出结论.
解答 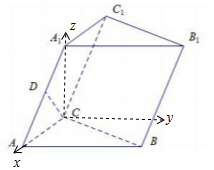 (1)证明:∵面ACC1A1⊥面ABC,AB⊥AC,
(1)证明:∵面ACC1A1⊥面ABC,AB⊥AC,
∴AB⊥面ACC1A1,即有AB⊥CD;
又AC=A1C,D为AA1中点,则CD⊥AA1.
∴CD⊥面ABB1A1.
(2)解:如图所示以点C为坐标系原点,CA为x轴,CA1为z轴,建立空间直角坐标系C-xyz,则有A(a,0,0),B(a,a,0),A1(0,0,a),B1(0,a,a),C1(-a,0,a),
设E(x,y,z),且$\overrightarrow{BE}=λ\overrightarrow{B{B_1}}$,即有(x-a,y-a,z)=λ(-a,0,a),
所以E点坐标为((1-λ)a,a,λa).
由条件易得面A1C1A的一个法向量为$\overrightarrow{n_1}=(0,1,0)$.
设平面EA1C1的一个法向量为$\overrightarrow{n_2}=(x,y,z)$,
由$\left\{\begin{array}{l}\overrightarrow{n_2}⊥\overrightarrow{{A_1}{C_1}}\\ \vec n⊥\overrightarrow{{A_1}E}\end{array}\right.$可得$\left\{\begin{array}{l}-ax=0\\(1-λ)ax+ay+(λ-1)az=0\end{array}\right.$,
令y=1,则有$\overrightarrow{n_2}=(0,1,\frac{1}{1-λ})$,
则$cos\frac{π}{3}=|\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}|$=$\frac{1}{{\sqrt{1+\frac{1}{{{{(1-λ)}^2}}}}}}=\frac{1}{2}$,得$λ=1-\frac{{\sqrt{3}}}{3}$.
所以,当$\frac{{|\overrightarrow{BE}|}}{{|\overrightarrow{B{B_1}}|}}=1-\frac{{\sqrt{3}}}{3}$时,二面角E-A1C1-A的大小为$\frac{π}{3}$.
点评 本题考查了线面垂直的性质与判断,考查了二面角的计算,属于中档题,解题时要认真审题,注意向量法的合理运用.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
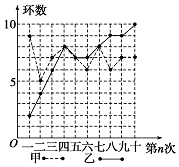 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com