
 如图,CD是圆O的切线,切点为D,CA是过圆心的割线且交圆O于B点,过B作⊙O的切线交CD于点E,DE=$\frac{1}{2}$EC.求证:
如图,CD是圆O的切线,切点为D,CA是过圆心的割线且交圆O于B点,过B作⊙O的切线交CD于点E,DE=$\frac{1}{2}$EC.求证:分析 (1)由切割线定理可得CD2=CA•CB,连接OD,根据切线的性质及切线长定理可得OD⊥CD,BE=ED,结合已知中DE=$\frac{1}{2}$EC,易得∠C=30°,进而可得CA=3CB;
(2)将CA=3CB代入CD2=CA•CB,化简可得:CA=$\sqrt{3}$CD.
解答 证明:(1)∵CD是圆O的切线,
∴CD2=CA•CB,
连结OD,则OD⊥CD,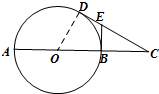
∵BE是圆O的切线,
∴BE=ED,
又$DE=\frac{1}{2}EC$,
∴$BE=\frac{1}{2}EC$,
∴∠C=30°,
则$OD=\frac{1}{2}OC$,
而OB=OD,
∴CB=BO=OD=OA,
∴CA=3CB,…(5分)
(2)将CA=3CB代入CD2=CA•CB得$C{D^2}=CA•\frac{1}{3}CA$,
故$CA=\sqrt{3}CD$.…(10分)
点评 本题考查的知识点是切割线定理,切线长定理,切线的性质,是与圆有关比例线段的综合应用,难度中档.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(理)试卷(解析版) 题型:选择题
设双曲线
 的右焦点为
的右焦点为 ,过点
,过点 与
与 轴垂直的直线
轴垂直的直线 交两渐近线于
交两渐近线于 ,
, 两点,与双曲线的其中一个交点为
两点,与双曲线的其中一个交点为 ,设坐标原点为
,设坐标原点为 ,若
,若
 ,且
,且 ,则该双曲线的渐近线为( )
,则该双曲线的渐近线为( )
A. B.
B. C.
C. D.
D. 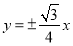
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com