
已知函数 .
.
(1)若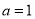 ,求函数
,求函数 的单调区间;
的单调区间;
(2)设函数 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
(1)递增区间是(?∞,? ),(0,+∞);递减区间是(?
),(0,+∞);递减区间是(? ,0).(2)[-
,0).(2)[- ,+
,+ ).
).
【解析】
试题分析:(1)求出 导函数,解出当
导函数,解出当 =1时,
=1时, >0对应的区间就是
>0对应的区间就是 的增区间,
的增区间, <0对应的区间就是
<0对应的区间就是 的减区间;(2)由函数
的减区间;(2)由函数 在区间
在区间 上是增函数知
上是增函数知 ≥0对
≥0对 ∈[1,2]恒成立,通过参变分离化为a≥?
∈[1,2]恒成立,通过参变分离化为a≥? 对
对 ∈[1,2]恒成立,求出?
∈[1,2]恒成立,求出? 在
在 ∈[1,2]上的最大值,则a大于等于?
∈[1,2]上的最大值,则a大于等于? 在
在 ∈[1,2]上的最大值,即得到a的取值范围.
∈[1,2]上的最大值,即得到a的取值范围.
试题解析:  =
= ,
,
(1)当a=1时, =
= ,
,
令 =0得x=0或x=?
=0得x=0或x=?
∴当 变化时,
变化时, ,
, 的变化情况如下表
的变化情况如下表
| (?∞,? | ? | (? | 0 | (0,+∞) |
| + | 0 | - | 0 | + |
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴ 的递增区间是(?∞,?
的递增区间是(?∞,? ),(0,+∞);递减区间是(?
),(0,+∞);递减区间是(? ,0).
,0).
(2)∵函数 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
∴对任意的 ∈[1,2]恒有
∈[1,2]恒有 ≥0,即对任意的
≥0,即对任意的 ∈[1,2]恒有a≥?
∈[1,2]恒有a≥?
∴a≥[? ]max,而函数y=?
]max,而函数y=? 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,
∴当 =1时,函数y=?
=1时,函数y=? 取最大值?
取最大值? ,
,
∴a≥? .
.
∴ 的取值范围为[-
的取值范围为[- ,+
,+ ).
).
考点:常见函数的导数,导数与函数单调性关系,恒成立问题,转化思想


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2015届江西省九江市七校高二下学期期中联考文科数学试卷(解析版) 题型:选择题
下表是降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出 关于
关于 的线性回归方程:
的线性回归方程: ,那么表中
,那么表中 的值为( )
的值为( )

A.3 B.3.15 C.4.5 D.4
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
(坐标系与参数方程选做题)在极坐标系中,点 到直线
到直线 的距离是 。
的距离是 。
A. B.3 C.1 D.2
B.3 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知i为虚数单位,复数 ,则复数
,则复数 在复平面上的对应点位于( )
在复平面上的对应点位于( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
甲、乙两套设备生产的同类型产品共4800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为 件.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
根据如下样本数据
x | 3 | 4 | 5 | 6 | 7 | 8 |
y | 4.0 | 2.5 |
| 0.5 |
|
|
得到的回归方程为 ,则 ( )
,则 ( )
A. ,
, B.
B. ,
,
C. ,
, D.
D. ,
,
查看答案和解析>>
科目:高中数学 来源:2015届江西省上饶市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某工厂生产某种零件,零件质量采用电脑自动化控制,某日生产100个零件,记产生出第n个零件时电脑显示的前n个零件的正品率为f(n),则下列关系式不可能成立的是( )
A.f(1)<f(2)< <f(100)
B.存在n {1,2, ,99},使得f(n)=2f(n+1)
{1,2, ,99},使得f(n)=2f(n+1)
C.存在n {1,2, ,98},使得f(n)<f(n+1),且f(n+1)=f(n+2)
{1,2, ,98},使得f(n)<f(n+1),且f(n+1)=f(n+2)
D.f(1)=f(2)= =f(100)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com