
分析 (1)利用函数y=f(x+1)是偶函数,求函数f(x)的解析式;
(2)利用复合函数的单调性,求实数b的值;
(3)分类讨论,求出函数的最小值,利用h(x)在区间[0,2]上有最小值为-2,得出结论.
解答 解:(1)∵函数y=f(x+1)是偶函数,
∴(x+1)2+a(x+1)+1=(-x+1)2+a(-x+1)+1,
∴4x+2ax=0,
∴a=-2,
∴f(x)=(x-1)2;
(2)g(x)=-b•f(f(x+1))+(3b-1)•f(x+1)+2=-bx4+(5b-1)x2+2-b,
令t=x2,u(t)=-bt2+(5b-1)t-(b-2),
在区间(-∞,-2]上,t=x2是减函数,且t∈[4,+∞),由g(x)是减函数,可知u(t)为增函数;
在区间(-2,0)上,t=x2是减函数,且t∈(0,4),由g(x)是增函数,可知u(t)为减函数,
∴由u(t)在(0,4)上是减函数,(4,+∞)上是增函数,
可得二次函数开口向上,b<0,且-$\frac{5b-1}{-2b}$=4,∴b=-$\frac{1}{3}$;
(3)h(x)=f(x+1)-2qx+1+2q=x2=2qx+2q,x∈[0,2].
q<0,ymin=h(0)=1+2q=-2,q=-$\frac{3}{2}$;
0≤q≤2,ymin=h(q)=-q2+2q+1=-2,∴q=3或-1,舍去;
q>2,ymin=h(2)=-2q+5=-2,q=$\frac{7}{2}$,
综上所述,q=-$\frac{3}{2}$或$\frac{7}{2}$.
点评 本题考查函数的性质,考查函数解析式的求解,考查学生的最值,正确分类讨论是关键.


科目:高中数学 来源: 题型:解答题
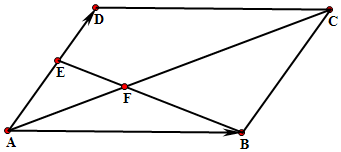 如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.
如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y>z | B. | y>x>z | C. | z>x>y | D. | x>z>y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 160 | C. | 180 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com