
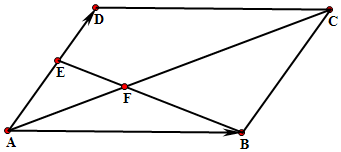
 如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.
如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.分析 (1)根据向量的线性运算,用向量$\overrightarrow{a},\overrightarrow{b}$分别表示出$\overrightarrow{CE}$,$\overrightarrow{BE}$.
(2)根据F的位置结合向量共线进行分类讨论,联立方程组求解.
解答 (本小题满分12分)
解:(I)$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.
∴$\overrightarrow{CE}=\overrightarrow{CD}+\overrightarrow{DE}$=$-\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$,…(2分)
$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}$=$-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,…(4分)
∴$\overrightarrow{CE}+\overrightarrow{BE}=-2\overrightarrow{a}$;…(6分)
(II)不妨设在线段AD上有满足条件的点E,则$\overrightarrow{AE}=λ\overrightarrow{b}$(0≤λ≤1)
(1)若$\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BE}$,则$\overrightarrow{BF}=\frac{1}{3}(-\overrightarrow{a}+\frac{1}{3}λ\overrightarrow{b})$,
∴$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}$=$\frac{2}{3}\overrightarrow{a}+\frac{1}{3}λ\overrightarrow{b}$…(7分)
又$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$,
且$\overrightarrow{AC}$与$\overrightarrow{AF}$是共线向量,则$\overrightarrow{AF}=μ\overrightarrow{AC}$
∴$\frac{2}{3}\overrightarrow{a}+\frac{1}{3}λ\overrightarrow{b}=μ(\overrightarrow{a}+\overrightarrow{b})$…(8分)
∵$\overrightarrow{a},\overrightarrow{b}$是不共线的向量,
∴$\left\{\begin{array}{l}{\frac{2}{3}=μ}\\{\frac{1}{3}λ=μ}\end{array}\right.$∴$\left\{\begin{array}{l}{λ=2}\\{μ=\frac{2}{3}}\end{array}\right.$
此时λ=2与0≤λ≤1矛盾,舍去;…(9分)
(2)若$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BE}$,则$\overrightarrow{BF}=\frac{2}{3}(-\overrightarrow{a}+λ\overrightarrow{b})$,
∴$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}=\frac{1}{3}\overrightarrow{a}+\frac{2}{3}λ\overrightarrow{b}$…(10分)
又$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$,
且$\overrightarrow{AC}$与$\overrightarrow{AF}$是共线向量,则$\overrightarrow{AF}=μ\overrightarrow{AC}$
∴$\frac{1}{3}\overrightarrow{a}+\frac{2}{3}λ\overrightarrow{b}=μ(\overrightarrow{a}+\overrightarrow{b})$…(11分)
∵$\overrightarrow{a},\overrightarrow{b}$是不共线的向量,
∴$\left\{\begin{array}{l}{\frac{1}{3}=μ}\\{\frac{2}{3}λ=μ}\end{array}\right.$,∴$\left\{\begin{array}{l}{λ=\frac{1}{2}}\\{μ=\frac{1}{3}}\end{array}\right.$
此时满足0≤λ≤1,
故满足条件的点E是存在的,它是线段AD的中点.…(12分)
点评 考查平面向量基本定理,平面向量线性运算,共线问题.考查分类讨论思想.根据向量共线构造方程组,是解决问题的关键.属于难题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 充分而不必要条件 | D. | 必要而不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设计一个计算1×3×5×7×9×11×13的算法.下面给出了程序的一部分,则在横线①上不能填入下面的哪一个数( )
设计一个计算1×3×5×7×9×11×13的算法.下面给出了程序的一部分,则在横线①上不能填入下面的哪一个数( )| A. | 13 | B. | 13.5 | C. | 14 | D. | 14.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1) | B. | [0,1) | C. | [-1,1] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com