
分析 (1)求出函数的导数,求出极值点,利用函数的单调性,求解函数的极值.
(2)求出函数f(x)的定义域,函数的导数,通过当a≤0时,当a>0时,分别求解函数的单调区间即可.
解答 解:(1)当a=1时,f(x)=lnx-x+3,$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$(1分)
令f'(x)>0解得0<x<1,所以函数f(x)在(0,1)单调递增; (2分)
令f'(x)<0解得x>1,所以函数f(x)在(1,+∞)单调递增; (3分)
所以当x=1时取极大值,极大值为f(1)=2;函数无极小值. (4分)
(2)函数f(x)的定义域为(0,+∞),$f'(x)=\frac{1}{x}-a$; (5分)
当a≤0时,$f'(x)=\frac{1}{x}>0$在(0,+∞)恒成立,所以函数f(x)在(0,+∞)单调递增;(7分)
当a>0时
令f'(x)>0解得$0<x<\frac{1}{a}$,所以函数f(x)在$(0,\frac{1}{a})$单调递增;
令f'(x)<0解得$x>\frac{1}{a}$,所以函数f(x)在$(\frac{1}{a},+∞)$单调递减;(10分)
综上所述:当a≤0时,函数f(x)的单调增区间为(0,+∞)
当a>0时,函数f(x)的单调增区间为$(0,\frac{1}{a})$,单调减区间为$(\frac{1}{a},+∞)$ (12分)
点评 本题考查函数的导数求解函数的极值,函数的单调性的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
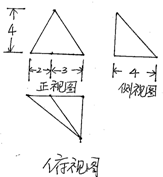
| A. | $\frac{80}{\begin{array}{l}3\end{array}}$ | B. | $\frac{40}{\begin{array}{l}3\end{array}}$ | C. | 80 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,-11) | B. | (-3,3) | C. | (4,-11)或(-3,3) | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
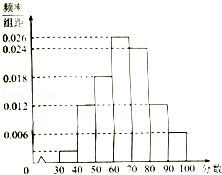 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com