
分析 先利用线面平行的判定定理证明直线C1A∥平面BDE,再将线面距离转化为点面距离,最后利用等体积法求点面距离即可.
解答 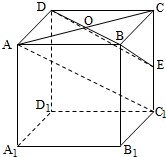 解:如图:连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,
解:如图:连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,
从而C1A∥平面BDE,
∴直线AC1与平面BED的距离即为点A到平面BED的距离,设为h,
在三棱锥E-ABD中,VE-ABD=$\frac{1}{3}$S△ABD×EC=$\frac{1}{3}$×$\frac{1}{2}$×2×2×$\sqrt{2}$=$\frac{2\sqrt{2}}{3}$
在三棱锥A-BDE中,BD=2$\sqrt{2}$,BE=$\sqrt{6}$,DE=$\sqrt{6}$,
∴S△EBD=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{6-2}$=2
∴VA-BDE=$\frac{1}{3}$×S△EBD×h=$\frac{1}{3}$×2$\sqrt{2}$×h=$\frac{2\sqrt{2}}{3}$
∴h=1
故答案为:1.
点评 本题主要考查了线面平行的判定,线面距离与点面距离的转化,三棱锥的体积计算方法,等体积法求点面距离的技巧,属于中档题


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
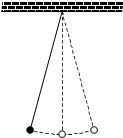 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 非统计专业 | 统计专业 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com