
分析 利用有理数指数幂性质、运算法则求解.
解答 解:$\frac{{(2×\root{3}{a^2}•\sqrt{b})(-6×\sqrt{a}•\root{3}{b})}}{{-3×\root{6}{a}•\root{6}{b^5}}}$
=$\frac{-12{a}^{\frac{2}{3}+\frac{1}{2}}•{b}^{\frac{1}{2}+\frac{1}{3}}}{-3×{a}^{\frac{1}{6}}{b}^{\frac{5}{6}}}$
=4a.
故答案为:4a.
点评 本题考查有理数指数幂化简求值,是基础题,解题时要认真审题,注意有理数指数幂性质、运算法则的合理运用.


科目:高中数学 来源: 题型:选择题
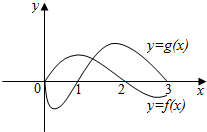 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )| A. | (0,1)∪(2,3) | B. | (-2,-1)∪(0,1)∪(2,3) | ||
| C. | (-1,0)∪(-3,-2)∪(0,1)∪(2,3) | D. | (-3,-1)∪(0,1)∪(2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
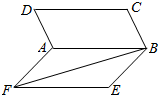 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com