
分析 直接写出全程命题的否定判断(1);举例说明(2)(3)错误;求出函数的值域判断(4).
解答 解:对于(1),命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0”,故(1)是真命题;
对于(2),若A>B,则sinA>sinB,是假命题,如A=390°,B=60°;
对于(3),已知数列{an},由an,an+1,an+2成等比数列成等比数列有$a_{n+1}^2={a_n}{a_{n+2}}$,反之,由$a_{n+1}^2={a_n}{a_{n+2}}$,不一定有an,an+1,an+2成等比数列,
如an=0,an+1=0,an+2=1,∴“an,an+1,an+2成等比数列”是“$a_{n+1}^2={a_n}{a_{n+2}}$”的充分不必要条件,故(3)是假命题;
对于(4),函数$f(x)=lgx+\frac{1}{lgx}$的值域为(-∞,-2]∪[2,+∞),故(4)是假命题.
∴真命题的序号为(1).
故答案为:(1).
点评 本题考查命题的真假判断与应用,考查充分必要条件的判定方法,考查函数值域的求法,是基础题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | (-$\frac{2}{e}$,2e) | D. | [-$\frac{3}{e}$,3e] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p | C. | p∧(?q) | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},1)$ | B. | (1,4) | C. | (4,8) | D. | (8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
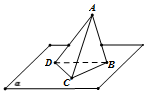 如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.
如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com