
| A�� | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B�� | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C�� | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 | D�� | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 |
���� �������⣬��Ҫ��˫���ߵķ���Ϊ$\frac{{x}^{2}}{2}$-y2=k����Ͻ����λ�ÿɵ�k��0���ɵ��������Ϊ��$\frac{{y}^{2}}{-k}$-$\frac{{x}^{2}}{-2k}$=1����˫���ߵļ������ʿɵ�c2=��-k��+��-2k��=36����ɵ�k��ֵ������˫���ߵı����̼��ɵô𰸣�
��� �⣺�������⣬Ҫ��˫������$\frac{{x}^{2}}{2}$-y2=1����ͬ�Ľ����ߣ��������䷽��Ϊ��$\frac{{x}^{2}}{2}$-y2=k��
�����佹��Ϊ��0��6�������佹����y������c=6������k��0��
�����������$\frac{{y}^{2}}{-k}$-$\frac{{x}^{2}}{-2k}$=1��
����c2=��-k��+��-2k��=36��
��ɵ�k=-12��
��Ҫ��˫���ߵı�����Ϊ��$\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1��
��ѡ��B��
���� ���⿼��˫���ߵļ������ʣ��漰˫���ߵı����̣��ؼ������ս�������ͬ��˫���߷��̵��跨��


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ҫ���� | B�� | ��ֶ�����Ҫ���� | ||
| C�� | ��Ҫ����������� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����������ABCD-A1B1C1D1�У�AB=4��M��N�ֱ�Ϊ��A1D1��A1B1���е㣬����B��ƽ�����ƽ��AMN����ƽ����ظ����������ý�������Ϊ18��
��ͼ��ʾ����������ABCD-A1B1C1D1�У�AB=4��M��N�ֱ�Ϊ��A1D1��A1B1���е㣬����B��ƽ�����ƽ��AMN����ƽ����ظ����������ý�������Ϊ18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
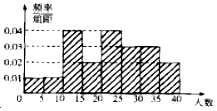 Ϊ�˸��õ���ѧ����Ӧ�߿������ľ���ijѧУ��Ը�У20���༶�����ˡ�������Ӣ���鷨��������ÿ���༶ֻ��һ��ָ����ʦ�����������˸���μӸñ�����ѧ�������������������ݣ������[0��5����[5��10����[10��15����[15��20����[20��25����[25��30����[30��35����[35��40]ʱ��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��
Ϊ�˸��õ���ѧ����Ӧ�߿������ľ���ijѧУ��Ը�У20���༶�����ˡ�������Ӣ���鷨��������ÿ���༶ֻ��һ��ָ����ʦ�����������˸���μӸñ�����ѧ�������������������ݣ������[0��5����[5��10����[10��15����[15��20����[20��25����[25��30����[30��35����[35��40]ʱ��������Ƶ�ʷֲ�ֱ��ͼ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -6 | B�� | -1 | C�� | 1 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 2011 | 2012 | 2013 | 2014 | 2015 |
| ʱ�����t | 1 | 2 | 3 | 4 | 5 |
| ������y��ǧ��Ԫ�� | 5 | 6 | 7 | 8 | 10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com