Question

17．已知曲线C₁的参数方程是$\left\{\begin{array}{l}{x=-2+2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C₂的极坐标方程是ρ=4sinθ．
（Ⅰ）求曲线C₁与C₂交点的平面直角坐标；
（Ⅱ）A，B两点分别在曲线C₁与C₂上，当|AB|最大时，求△OAB的面积（O为坐标原点）．

Answer 1

分析 （Ⅰ）求出曲线C₁，C₁的平面直角坐标方程，把两式作差，得y=-x，代入x²+y²=4y，能求出曲线C₁与C₂交点的平面直角坐标．
（Ⅱ）作出图形，由平面几何知识求出当|AB|最大时|AB|=2$\sqrt{2}+4$，O到AB的距离为$\sqrt{2}$，由此能求出△OAB的面积．

解答 解：（Ⅰ）∵曲线C₁的参数方程是$\left\{\begin{array}{l}{x=-2+2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），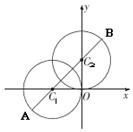
∴曲线C₁的平面直角坐标方程为（x+2）²+y²=4．
又由曲线C₂的极坐标方程是ρ=4sinθ，
得ρ²=4ρsinθ，∴x²+y²=4y，
把两式作差，得y=-x，
代入x²+y²=4y，得2x²+4x=0，
解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$，
∴曲线C₁与C₂交点的平面直角坐标为（0，0），（-2，2）．
（Ⅱ）如图，由平面几何知识可知：
当A，C₁，C₂，B依次排列且共线时，
|AB|最大，此时|AB|=2$\sqrt{2}+4$，
O到AB的距离为$\sqrt{2}$，
∴△OAB的面积为S=$\frac{1}{2}（2\sqrt{2}+4）•\sqrt{2}=2+2\sqrt{2}$．

点评 本题考查两曲线交点的平面直角坐标的求法，考查三角形面积的求法，是中档题，解题时要认真审题，注意参数方程、直角坐标方程、极坐标方程间的相互转化及应用．