
 在三棱锥P-ABC中,△PAB是等边三角形,∠APC=∠BPC=60°.
在三棱锥P-ABC中,△PAB是等边三角形,∠APC=∠BPC=60°.分析 (Ⅰ)先证AB⊥平面PDC,再由线面垂直的性质证明AB⊥PC;
(Ⅱ)求出底面面积,以及高,转化求VP-ABE,即可.
解答 解:(Ⅰ)证明:如图,取AB的中点D,连结PD,CD,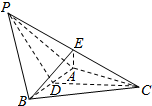
则PD⊥AB,CD⊥AB,
∴AB⊥平面PDC,PC?平面PDC,
∴AB⊥PC;
(Ⅱ)连结AE.BE⊥PC,
∵△PAB是等边三角形,∴AE⊥PC,AB⊥PC,PC⊥平面EAB,
PB=4,AB=PA=4,∠APC=∠BPC=60°,可得PE=2,BE=AE=2$\sqrt{3}$,DE=2$\sqrt{2}$.
∴VP-ABE=$\frac{1}{3}$×$\frac{1}{2}×$2$\sqrt{2}$×4×2=$\frac{8\sqrt{2}}{3}$.
点评 本题考查了线面垂直的证明与性质,考查了棱锥的体积计算,考查了学生的推理论证能力及空间想象能力.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:填空题
 如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.
如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
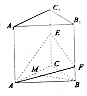 如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com