
分析 (Ⅰ)当a=1,b=2时,把不等式f(x)<4转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)利用绝对值三角不等式、基本不等式求得f(x)的最小值为$\frac{9}{2}$,从而证得结论,此时,由b=2a,$\frac{1}{2a}+\frac{2}{b}=1$,解得a,b的值.
解答 解:(Ⅰ)当a=1,b=2时,不等式f(x)<4化为|x+1|+|x-2|<4,
即$\left\{\begin{array}{l}{x<-1}\\{-x-1+2-x<4}\end{array}\right.$①,或$\left\{\begin{array}{l}{-1≤x≤2}\\{x+1+2-x<4}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{x>2}\\{x+1+x-2<4}\end{array}\right.$ ③.
解①求得-$\frac{3}{2}$<x<-1,解②求得-1≤x≤2,解③求得2≤x<$\frac{5}{2}$,
∴不等式f(x)<4的解集为$\{x|-\frac{3}{2}<x<\frac{5}{2}\}$.
(Ⅱ)证明:f(x)=|x+a|+|x-b|≥|(x+a)-(x-b)|=|a+b|=a+b
=$(a+b)(\frac{1}{2a}+\frac{2}{b})$=$\frac{5}{2}+\frac{b}{2a}+\frac{2a}{b}$$≥\frac{5}{2}+2\sqrt{\frac{b}{2a}•\frac{2a}{b}}$=$\frac{9}{2}$,
当且仅当$\frac{b}{2a}=\frac{2a}{b}$,即b=2a时“=”成立.
又当f(x)=$\frac{9}{2}$时,b=2a,$\frac{1}{2a}+\frac{2}{b}=1$,解得$a=\frac{3}{2}$,b=3.
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式和基本不等式的应用,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
 如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.
如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -1 | C. | 1 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
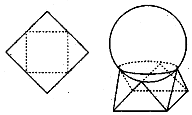 如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )
如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{\sqrt{6}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
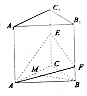 如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com