
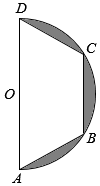
 如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.
如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积. 分析 几何体为球体减去两个圆锥和一个圆柱后剩余的部分,使用作差法求出体积.
解答 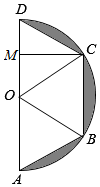 解:连结OB,OC,∵BC=$\frac{1}{2}$AB=OB=OC=2,CD=AB
解:连结OB,OC,∵BC=$\frac{1}{2}$AB=OB=OC=2,CD=AB
∴△OBC,△OCD,△OAB是等边三角形,
过C作CM⊥AD,则CM=$\sqrt{3}$,DM=1,
∴阴影部分绕AD旋转一周所得几何体为球体减去两个圆锥和一个圆柱后剩余部分.
圆柱和圆锥的底面半径为CM=$\sqrt{3}$,圆柱的高为BC=2,圆锥的高为DM=1.
球的半径为$\frac{1}{2}$AB=2.
∴几何体体积V=V球-2V圆锥-V圆柱=$\frac{4}{3}π×{2}^{3}$-2×$\frac{1}{3}π×3×1$-π×3×2=$\frac{8π}{3}$.
点评 本题考查了旋转体的结构特征,体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
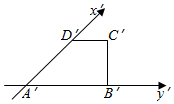 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|=|$\overline{{z}_{1}}$|=$\sqrt{{{z}_{1}}^{2}}$ | |
| B. | 若|z2|=2,则z2的取值集合为{-2,2,-2i,2i}(i是虚数单位) | |
| C. | 若z12+z22=0,则z1=0或z2=0 | |
| D. | z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2一定是实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com