
分析 由已知利用等比数列的性质、等比中项的定义先求出a2,进而求出公比,由此能求出a4的值.
解答 解:∵在等比数列中,a1=9,a2是3和12的等比中项,
∴${{a}_{2}}^{2}=3×12$=36,
解得a2=6或a2=-6,
当a2=6时,q=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{6}{9}$=$\frac{2}{3}$,${a}_{4}={a}_{1}{q}^{3}=9×(\frac{2}{3})^{3}$=$\frac{8}{3}$;
当a2=-6时,q=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{-6}{9}$=-$\frac{2}{3}$,${a}_{4}={a}_{1}{q}^{3}$=9×(-$\frac{2}{3}$)3=-$\frac{8}{3}$.
点评 本题考查等比数列的第4项的求法,是基础题,解题时要认真审题,注意等比数列的性质、等比中项的定义的合理运用.


科目:高中数学 来源: 题型:解答题
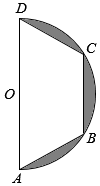 如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.
如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-3y-5=0 | B. | 3x+y-5=0 | C. | x+3y-5=0 | D. | x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
| 质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天数K | 5 | 23 | 22 | 25 | 15 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com