
分析 求出$\overrightarrow{a},\overrightarrow{b}$的夹角,建立平面直角坐标系,设$\overrightarrow{a}$=(2,0),则$\overrightarrow{b}$=(1,$\sqrt{3}$),根据数量积的几何意义得出C的轨迹,利用点到圆的最短距离求出|2$\overrightarrow{b}$-$\overrightarrow{c}$|的最小值.
解答 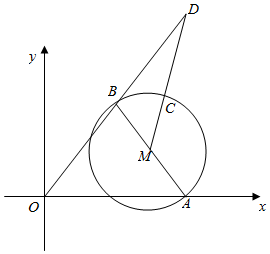 解:∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\overrightarrow{a}$•$\overrightarrow{b}$=2,∴cos<$\overrightarrow{a},b$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2}$,
解:∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\overrightarrow{a}$•$\overrightarrow{b}$=2,∴cos<$\overrightarrow{a},b$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2}$,
∴<$\overrightarrow{a},\overrightarrow{b}$>=60°.
设$\overrightarrow{OA}=\overrightarrow{a}$=(2,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(1,$\sqrt{3}$),$\overrightarrow{OC}=\overrightarrow{c}$,
∵($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,
∴$\overrightarrow{CA}⊥\overrightarrow{CB}$,∴C的轨迹为以AB为直径的圆M.
其中M($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),半径r=1.
延长OB到D,则D(2,2$\sqrt{3}$).连结DM,交圆M于C点,则CD为|2$\overrightarrow{b}$-$\overrightarrow{c}$|的最小值.
DM=$\sqrt{(2-\frac{3}{2})^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{7}$.
∴CD=$\sqrt{7}-1$.
故答案为:$\sqrt{7}$-1.
点评 本题考查了平面向量的数量积运算,平面向量的几何意义,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | |z1|=|$\overline{{z}_{1}}$|=$\sqrt{{{z}_{1}}^{2}}$ | |
| B. | 若|z2|=2,则z2的取值集合为{-2,2,-2i,2i}(i是虚数单位) | |
| C. | 若z12+z22=0,则z1=0或z2=0 | |
| D. | z1$\overline{{z}_{2}}$+$\overline{{z}_{1}}$z2一定是实数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
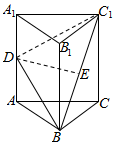 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 10 |
| A. | 16个 | B. | 20个 | C. | 24个 | D. | 28个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com